A simplified graphical approach to machine learning
November 14, 2013
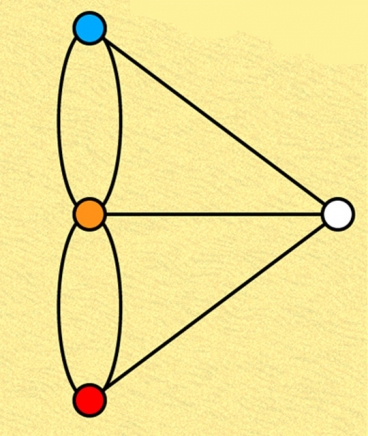
Graph theory is generally thought of as originating with the “Königsberg bridge problem,” which asked whether a walker could cross the seven bridges of Königsberg, Prussia (now Kaliningrad, Russia), once each without crossing any of them twice. This is the graphical depiction of the problem, where the nodes represent land masses and the edges bridges. (Credit: Horatius/Wikimedia Commons)
An algorithm that extends an artificial-intelligence technique to new tasks could aid in analysis of flight delays and social networks.
Much artificial-intelligence research is concerned with finding statistical correlations between variables: What combinations of visible features indicate the presence of a particular object in a digital image? What speech sounds correspond with instances of what words? What medical, genetic, and environmental factors are correlated with what diseases?
As the number of variables grows, calculating their aggregate statistics becomes dauntingly complex. But that calculation can be drastically simplified if you know something about the structure of the data — that, for instance, the sound corresponding to the letter “T” is frequently followed by the sound corresponding to the letter “R,” but never by the sound corresponding to the letter “Q.”
In a paper being presented in December at the annual conference of the Neural Information Processing Systems Foundation, MIT researchers describe a new technique that expands the class of data sets whose structure can be efficiently deduced. Not only that, but their technique naturally describes the data in a way that makes it much easier to work with.
In the paper, they apply their technique to several sample data sets, including information about commercial airline flights. Using only flights’ scheduled and actual departure times, the algorithm can efficiently infer vital information about the propagation of flight delays through U.S. airports. It also identifies those airports where delays are most likely to have far-reaching repercussions, which makes it simpler to reason about the behavior of the network as a whole.
Thinking graphically
In technical terms, the researchers’ work concerns probabilistic graphical models. In this context, a graph is a mathematical construct that consists of nodes and edges, usually depicted as, respectively, circles and the lines that connect them. A network diagram is a familiar example of a graph; a family tree is another.
In a graphical model, the edges have an associated number, which describes the statistical relationship between the nodes. In the linguistic example, the nodes representing the sounds corresponding to “T” and “R” would be connected by a highly weighted edge, while the nodes corresponding to “T” and “Q” wouldn’t be connected at all.
Graphical models simplify reasoning about data correlations because they eliminate the need to consider certain dependencies. Suppose, for instance, that your artificial-intelligence algorithm is looking for diagnostically useful patterns in a mountain of medical data, where the variables include patients’ symptoms, their genetic information, their treatment histories, and prior diagnoses.
Without the graph structure, the algorithm would have no choice but to evaluate the relationships among all the variables at once. But if it knows, for instance, that gene “G” is a cause of disease “D,” which is treated with medication “M,” which has side effect “S,” then it has a much simpler time determining whether, for instance, “S” is a previously unidentified indicator of “D.” A graphical model is a way of encoding those types of relationships so that they can be understood by machines.
Historically, graphical models have sped up machine-learning algorithms only when they’ve had a few particular shapes, such as that of a tree. A tree is a graph with no closed loops: In a family tree, for instance, a closed loop would indicate something biologically impossible — that, say, someone is both parent and sibling to the same person.
Out of the loop
According to Ying Liu, a graduate student in MIT’s Department of Electrical Engineering and Computer Science who co-wrote the new paper with his advisor, Alan Willsky, the Edwin Sibley Webster Professor of Electrical Engineering, loops pose problems because they can make statistical inference algorithms “overconfident.” The algorithm typically used to infer statistical relationships within graphical models, Liu explains, is a “message-passing algorithm, where each node sends messages to only its neighbors, using only local information and incoming messages from other neighbors. It’s a very good way to distribute the computation.”
If the graph has loops, however, “a node may get some message back, but this message is partly from itself. So it gets overconfident about the beliefs.”
In prior work, Liu and Willsky showed that efficient machine learning can still happen in a “loopy” probabilistic graph, provided it has a relatively small “feedback vertex set” (FVS) — a group of nodes whose removal turns a loopy graph into a tree. In the airline-flight example, many of the nodes in the FVS were airline hubs, which have flights to a large number of sparsely connected airports. The same structure is seen in other contexts in which machine learning is currently applied, Liu says, such as social networking..
In the new paper, they show that the structure of a graphical model can be deduced by similar means. A structureless data set is equivalent to a graph in which every node is connected to every other node. Liu and Willsky’s algorithm goes through the graph, sequentially removing nodes that break loops and, using the efficient algorithm they demonstrated previously, calculating how close the statistical dependencies of the resulting graph are to those of the fully connected graph.
In this manner, the algorithm builds up an FVS for the graph. What remains is a tree — or something very close to a tree — that allows for efficient calculation. In practice, Liu and Willsky found that in order to make machine learning efficient, they required an FVS whose size was only about the logarithm of the total number of nodes in the graph.
Oscillations between problems
Sujay Sanghavi, an assistant professor of electrical and computer engineering at the University of Texas at Austin, has also studied the problem of learning the structure of graphical models. Of the MIT researchers’ work, Sanghavi says, “They kind of decompose the problem into two problems, each of which is much simpler to solve individually, and then they alternate between the two. That is a much better way to solve the problem than the original one, which has both issues mixed together.”
In cases where the FVS has been identified, Sanghavi says, “You can easily find the graph that does not include those nodes. That’s a cute observation, that once you have these nodes, the rest of the problem is easy. The other problem is also easy, which is, I give you only those nodes, which are a small number, and you need to find only those edges which have one of the endpoints as those nodes. It’s just when you try to solve both problems together that it becomes hard. That’s the main insight in this paper, and I think it’s quite nice.”
Sanghavi has recently been using graphical models to examine the structure of gene regulatory networks, and he’s curious to see whether the MIT researchers’ technique will apply to that problem. “Some genes fire and they fire other genes and so on,” Sanghavi explains. “Really what you want to do is find the dependence network between genes, and that can be posed as a Gaussian graphical-model learning problem. It would be interesting to see if their methods perform well.”