A theoretical metamaterial that acts as an analog computer
January 12, 2014
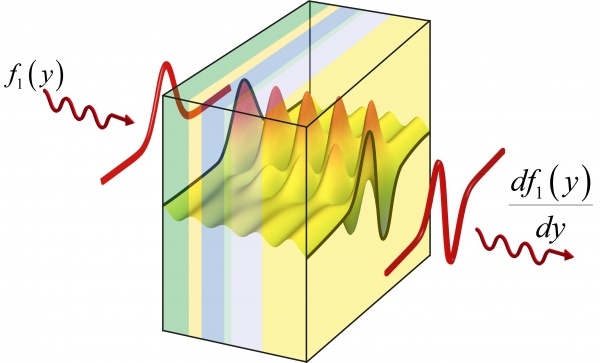
The curve of the incoming wave’s profile is transformed into that curve’s derivative (credit: Alexandre Silva)
Metamaterials can be designed to do “photonic calculus” as a light wave goes through them, researchers at the University of Pennsylvania, The University of Texas at Austin and University of Sannio in Italy have discovered.
A light wave, when described in terms of space and time, has a profile in space that can be thought of as a curve on a Cartesian (x,y) coordinate system.
The theoretical metamaterial can perform a specific mathematical operation on that wave’s profile, such as finding its first derivative (instantaneous rate of change) as the light wave passes through the material.
Essentially, shining a light wave on one side of such a material would result in that wave profile’s derivative exiting the other side. Metamaterials capable of other calculus operations, such as integration and convolution, could also be produced.
Viewing and manipulating this type of light-wave “profile” is an everyday occurrence for applications like image processing, though it is typically done after the light wave has been converted to electronic signals in the form of digital information. The researchers’ proposed computational metamaterials could almost instantly perform such operations on the original wave, such as the light coming in through the lens of a camera, without conversion to electronic signals.
Both mechanical and electronic analog computers were particularly suited to calculating large tables of information. Where the paper-and-pencil method would require tedious and repetitious steps performed on each of the table’s elements, with each step prone to human error, analog computers could perform those steps in parallel, producing the results all at once.
“Compared to digital computers, these analog computers were bulky, power hungry, and slow,“ said Nader Engheta, the H. Nedwill Ramsey professor of Electrical and Systems Engineering in Penn’s School of Engineering and Applied Science. “But by applying the concepts behind them to optical metamaterials, one day we might be able to make them at micro- and nanoscale sizes, and operate them at nearly speed of light using little power.”
“The thickness of our structures can be comparable with the optical wave length or even smaller,” said Vincenzo Galdi of the University of Sannio. “Implementing similar operations with conventional optical systems, such as lenses and filters, would require much thicker structures.”
How metamaterials work
By going to another layer of organization — making patterns of multiple materials at length scales smaller than the waves passing through them, like a series of nanoscopic gold cubes embedded in glass — metamaterial designers can alter waves in ways not possible by simple surfaces or lenses.
For example, a pen sticking out of a glass of water looks bent because the water surface refracts or “bends” the light; light traveling from the pen to the viewer from below the water line has a different angle of refraction than the light traveling from above.
Unlike natural materials, however, metamaterials can be designed to produce negative angles of refraction. If the water in the glass exhibits negative refraction, the image of the pen below the water line would not just be bent, but flipped as if viewed in a mirror. Metamaterials can also be designed for cloaking (hiding) an object.
Multiple such manipulations can be combined or performed in sequence, allowing metamaterial researchers to change the shape of waves in complex ways.
Analog computational tasks using metamaterials
Once built, these metamaterials could be put to use doing specific computational tasks that are best suited to an analog approach. Taking the derivative of an algebraic function, for example, is a task that digital computers must perform by brute force, essentially scanning the curve and evaluating the difference between every pair of neighboring points.
Even though modern digital computers can scan the 2-D profile very quickly, the time to complete the task increases along with the size of the profile. A computational metamaterial designed to calculate derivatives with light waves, by contrast, could complete the task nearly instantaneously regardless of the size of the profile, as it would operate on all points at once.
One analog-suited application that might make direct use of such computational metamaterials is edge detection, an image processing technique that helps software find faces and identify objects in pictures.
“When we do edge detection on an image now with currently available image processing techniques, we do it digitally, pixel by pixel,” Engheta said. “We scan an image and compare all of the neighboring pixels, and where there is a big difference between two, we label it an edge. With this computational metamaterial in the future, hopefully we will be able to do it all at once. The light from the image itself could go in and the edge-detected profile could come out the other side.”
“Thanks to recent advances in nanotechnology,” said Andrea Alù, Associate Professor and David & Doris Lybarger Endowed Faculty Fellow at The University of Texas at Austin, “today we are able to control light propagation through a material in unprecedented ways, and realize material functionalities that would have been unthinkable only a few years ago. In this paper, we set the stage to have metamaterials realize a broad set of mathematical operations for us on-the-fly, as light propagates through them.”
Future research will entail constructing and testing these computational metamaterials in laboratory settings. If successful, the researchers will draw up plans for metamaterials that can perform other mathematical operations, or even solve equations. By encoding the input wave with a mathematical function, then feeding the outgoing wave back to the input, the intervening metamaterial would ultimately produce a wave that would reveal the desired variables within that function.
The research was supported by the U.S. Office of Naval Research’s Multidisciplinary University Research Initiative.
Abstract of Science paper
