Can a robot pass the University of Tokyo math entrance exam?
September 13, 2012
(Credit: University of Tokyo)
Fujitsu Laboratories has announced it will participate in Japan’s National Institute of Informatics (NII) AI project, ”Can a Robot Pass the University of Tokyo (Todai) Entrance Exam?” (“Todai Robot”), led by NII professor Noriko Arai.
The goal of the project: enable an AI program to score high marks on Todai’s math entrance exam for admission by 2016, and meet all admission requirements for Todai by 2021.
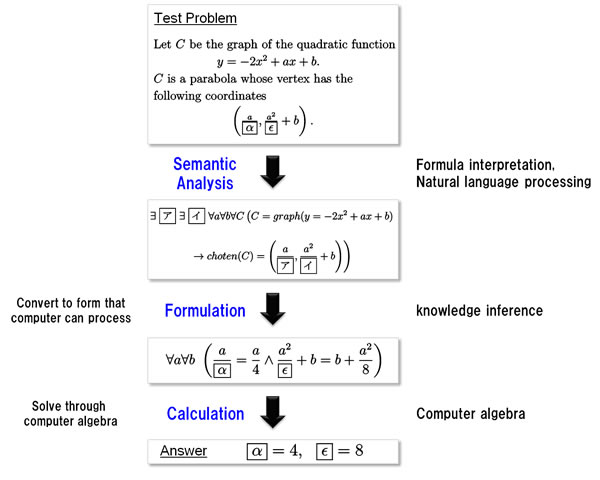
The test uses high-school math problems. For a computer to solve a math problem, it needs three things, according to NII:
- Semantic analysis: Understand the problem text, which is expressed as natural language and formulas easily understood by humans.
- Formulation: Convert to a form that can be processed by a computer.
- Calculation: Find the answer using the mathematical solver.
Procedure for solving math problems (credit: Fujitsu)
So far, Todai Robot can solve about 50–60% of Todai’s Level 2 entrance-exam problems, Fujitsu says.
Fujitsu Laboratories has been researching formula manipulation and computer algebra methods for exactly solving problems related to mathematical analysis and optimization technologies.
References:
- Akiko Aizawa, Takuya Matsuzaki, Hirokazu Anai, Uniting Natural Language Processing and Computer Algebra to Solve Mathematics Problems, Journal of the Japanese Society for Artificial Intelligence, 27(5), 2012, in press
Comments (7)
by Imants Vilks
Proposed solution does not contain the main task: “1. Semantic analysis: Understand the problem text, which is expressed as natural language and formulas easily understood by humans.”
To understand means the ability to create external world model and predict its reactions. In this case it means that the machine has to create:
1. A model for determining function’s maximum, minimum or bend point where derivative dy/dx = 0. In this case to solve the equation dy/dx= -4x+a=0, i.e., to find the xo coordinate xo=a/4.
2. A model for determining wether the found point is maximum, minimum or bend point: when the second derivative is positive, the function has its minimum, when it is negative, the function has maximum, and when it = 0, the function has a bend point. In this case to calculate the second derivative d2y/dx = -4. The second derivative is negative, the function has a minimum at xo=a/4.
3. A model for calculating the minimum point y coordinate: yo= f(xo) = -2×2+axo+b= a2/8 +b.
by Editor
NLP + Mathematica?
by superscenic
Hope it has babies soon.
by asiwel
Looked at this quickly … some folk might not recognize all the notation. So:
The parabola is given by y = -2xsquared + ax +b.
Set dy/dx = -4x + a =0. Solve for x = a/4. Replace x in equation and solve for b when y = 0 = -2asquared/16 + asquared/4 + b = asquared/8 + b.
The vertex of this parabola is a function of (a,b) and = (a/4, asquared/8 +b).
by Bri
I think the sixty four thousand dollar question is can the average student pass a high school math test. We are soooooo toast. Robots will be doing mental cartwheels around us soon.
by GatorALLin
…the computer was unable to write its name on the top of the test paper…..fail.
by Mr.X
Still better than some humans!Most of them don’t even get to the entrance exam.