Fujitsu Laboratories has announced it will participate in Japan’s National Institute of Informatics (NII) AI project, “Can a Robot Pass the University of Tokyo (Todai) Entrance Exam?” (“Todai Robot”), led by NII professor Noriko Arai.

The goal of the project: enable an AI program to score high marks on Todai’s math entrance exam for admission by 2016, and meet all admission requirements for Todai by 2021.

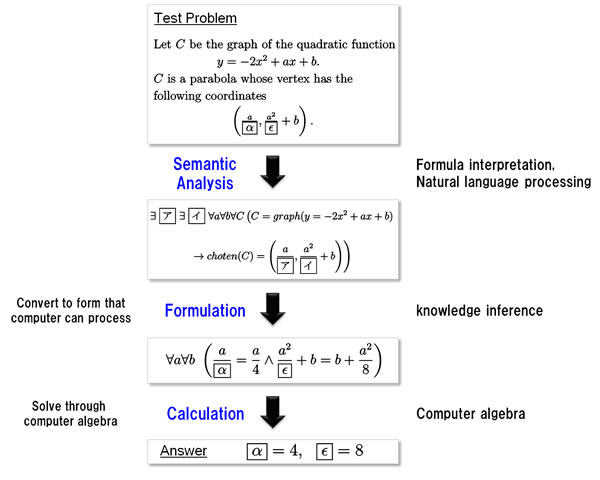
The test uses high-school math problems. For a computer to solve a math problem, it needs three things, according to NII:

1. Semantic analysis: Understand the problem text, which is expressed as natural language and formulas easily understood by humans.
2. Formulation: Convert to a form that can be processed by a computer.
3. Calculation: Find the answer using the mathematical solver.

So far, Todai Robot can solve about 50–60% of Todai’s Level 2 entrance-exam problems, Fujitsu says.

Fujitsu Laboratories has been researching formula manipulation and computer algebra methods for exactly solving problems related to mathematical analysis and optimization technologies.