Consciousness Connects Our Brains to the Fundamental Level of the Universe
May 14, 2001 by Stuart Hameroff
Neurons alone aren’t sufficiently complex to explain consciousness and provide a computational model for thought, according to Stuart Hameroff. He wants to go smaller, into a universe of structures within neurons where quantum mechanics help formulate a physical theory of consciousness.
Originally published May 14, 2001 on KurzweilAI.net.
Introduction: Brain=mind=computer?
What is consciousness? How are we different from machines? Why do we have thoughts, feelings and emotions?
Brain imaging technologies demonstrate anatomical location of activities which appear to correlate with consciousness, but which may not be directly responsible for consciousness.
We are left with the questions of what consciousness actually is, and how it is produced.
Most scientific explanations portray consciousness as an “emergent property” of classical computer-like activities in the brain’s neural networks. The prevailing views among scientists in this camp are that 1) patterns of neural network activities correlate with mental states, 2) synchronous neural network oscillations in thalamus and cerebral cortex temporally bind information, and 3) consciousness emerges as a novel property of computational complexity among neurons, somewhat like how music emerges from complex and highly organized movements of air molecules
However, these approaches appear to fall short in fully explaining certain enigmatic features of consciousness, such as:
- The nature of subjective experience, or ‘qualia’- our ‘inner life’ (Chalmers’ “hard problem”);
- Binding of spatially distributed brain activities into unitary objects in vision, and a coherent sense of self, or ‘oneness’;
- Transition from pre-conscious processes to consciousness itself;
- Non-computability, or the notion that consciousness involves a factor which is neither random, nor algorithmic, and that consciousness cannot be simulated (Penrose, 1989, 1994, 1997);
- Free will;
- Subjective time flow.
Conventional emergence approaches (also known as functionalist, reductionist, materialist, physicalist, computationalist approaches) argue that neurons and their chemical synapses are the fundamental units of information in the brain, and that conscious experience emerges when a critical level of complexity is reached in interactions among these fundamental units.
This basic conventional idea is that the mind is a computer functioning in the brain (brain = mind = computer). However in fitting the brain to a computational view, such explanations omit neurophysiological details such as:
- Widespread apparent randomness at all levels of neural processes (is it really noise, or underlying levels of complexity?);
- Glial cells (which account for some 80% of brain);
- Dendritic-dendritic processing (e.g. Pribram, Eccles);
- Electrotonic gap junctions which connect neuronal interiors;
- Cytoplasmic/cytoskeletal activities within neurons; and,
- Living state (the brain is alive!).
A further difficulty for the convenional brain=mind=computer approach is the absence of testable hypotheses in emergence theory. No threshold or rationale is specified; rather, consciousness “just happens.”
Finally, the complexity of individual neurons and synapses is not accounted for in such arguments. Treating neurons as indivisible units, switches or bit states is an insult to neurons. Cells are themselves highly complex and dynamical. For example, single cell protozoan organisms are able to swim, find food, and learn through the use of their internal cytoskeleton. Are such protozoa more intelligent than neurons?
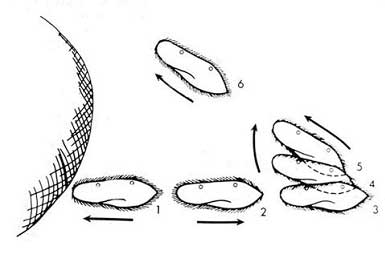
Figure 1. Single cell paramecium can swim and avoid obstacles using its cytoskeleton.
Inside Neurons — Microtubules and the Cytoskeleton
Activities within cells ranging from single-celled organisms to the brain’s neurons are organized by a dynamic scaffolding called the cytoskeleton, whose major components are microtubules. Hollow, crystalline cylinders 25 nanometers in diameter, microtubules are comprised of hexagonal lattices of proteins, known as tubulin. Microtubules are essential to cell shape, function, movement, and division. In neurons microtubules self-assemble to extend axons and dendrites and form synaptic connections, then help to maintain and regulate synaptic activity responsible for learning and cognitive functions. Microtubules interact with membrane structures mechanically by linking proteins, chemically by ions and “second-messenger” signals, and electrically by voltage fields.
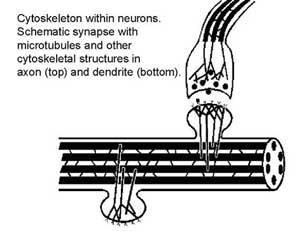
Figure 2. Schematic view of two neurons connected by chemical synapse. Axon terminal (above) releases neurotransmitter vesicles which bind receptors on post-synaptic dendritic spine. Within neurons are visible cytoskeletal structures microtubules (“MTs” – thicker tubes) as well as actin, synapsin and others which connect MTs to membranes. Also, MT-associated proteins (“MAPs”) interconnect MTs.
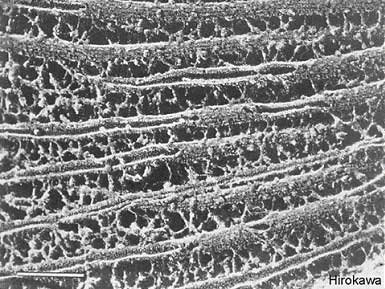
Figure 3. Immunoelectron micrograph of dendritic microtubules interconnected by MAPs. Some MTs have been sheared, revealing internal hollow core. The granular “corn-cob” surface of MTs is barely evident to close inspection. Scale bar, lower left: 100 nanometers. With permission from Hirokawa, 1991.
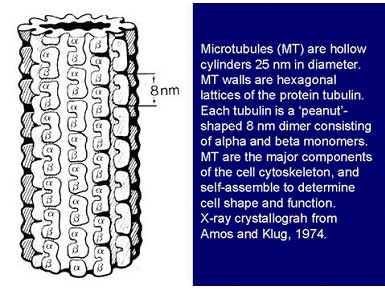
Figure 4. Crystallographic structure of microtubules.
While microtubules have traditionally been considered as purely structural elements, recent evidence has revealed that mechanical signaling and communication functions also exist:
- MT “kinks” travel at 15 microns (2000 tubulin subunits) per second. Vernon and Woolley (1995) Experimental Cell Research 220(2)482-494
- MTs vibrate (100-650 Hz) with nanometer displacement. Yagi, Kamimura, Kaniya (1994) Cell motility and the cytoskeleton 29:177-185
- MTs optically “shimmer” when metabolically active. Hunt and Stebbings (1994), Cell motility and the cytoskeleton 17:69-78
- Mechanical signals propogate through microtubules to cell nucleus; mechanism for MT regulation of gene expression. Maniotis, Chen and Ingber (1996) Proc. Natl. Acad. Sci. USA 94:849-854
- Measured tubulin dipoles and MT conductivity suggest MTs are ferroelectric at physiological temperature (Tuszynski; Unger 1998)
Current models propose that tubulins within microtubules undergo coherent excitation, switching between two or more conformational states in nanoseconds. Dipole couplings among neighboring tubulins in the microtubule lattice form dynamical patterns, or “automata,” which evolve, interact and lead to the emergence of new patterns. Research indicates that microtubule automata computation could support classical information processing, transmission and learning within neurons.
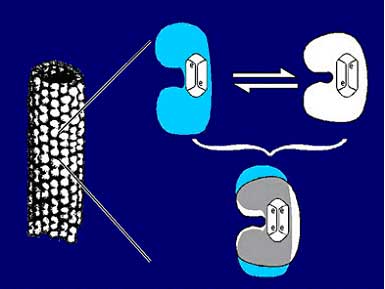
Figure 5. Left: Microtubule (MT) structure: a hollow tube of 25 nanometers diameter, consisting of 13 columns of tubulin dimers arranged in a skewed hexagonal lattice (Penrose, 1994). Right (top): Each tubulin molecule may switch between two (or more) conformations, coupled to London forces in a hydrophobic pocket. Right (bottom): Each tubulin can also exist (it is proposed) in quantum superposition of both conformational states.

Figure 6. Microtubule automaton simulation (from Rasmussen et al., 1990). Eight nanosecond time steps of a segment of one microtubule are shown in “classical computing” mode in which conformational states of tubulins are determined by dipole-dipole coupling between each tubulin and its six (asymmetrical) lattice neighbors. Conformational states form patterns which move, evolve, interact and lead to emergence of new patterns.
Microtubule automata switching offers a potentially vast increase in the computational capacity of the brain. Conventional approaches focus on synaptic switching at the neural level which optimally yields about 1018 operations per second in human brains (~1011 neurons/brain with ~104 synapses/neuron, switching at ~103 sec-1). Microtubule automata switching can explain some 1027 operations per second (~1011 neurons with ~107 tubulins/neuron, switching at ~109 sec-1). Indeed, the fact that all biological cells typically contain approximately 107 tubulins could account for the adaptive behaviors of single-celled organisms which have no nervous system or synapses. Rather than simple switches, neurons are complex information processing systems.
Panpsychism Meets Quantum Gravity (Plato at the Planck scale)
But how does a further level of information processing help explain consciousness? Greater computational complexity and ultra-reductionism to the level of microtubule automata don’t really explain enigmatic features of consciousness, in particular the nature of conscious experience; they merely facilitate emergence. Something more is required. If functional approaches and emergence are incomplete, perhaps the raw components of mental processes (qualia) are fundamental properties of nature (like mass, spin or charge). This view has long been held by panpsychists throughout the ages–for example Buddhists and Eastern philosophers claim a “universal mind.” Following the ancient Greeks, Spinoza argued in the 17th century that some form of consciousness existed in everything physical. The 19th century mathematician Leibniz proposed that the universe was composed of an infinite number of fundamental units, or “monads,” with each possessing a form of primitive psychological being. In the 20th century, Bertrand Russell claimed that there was a common entity underlying both mental and physical processes, while John Wheeler and David Chalmers have maintained that there exists an experiential aspect to fundamental information.
Of particular interest is the work of the 20th century philosopher Alfred North Whitehead, whose pan-experiential view remains most consistent with modern physics. Whitehead argued that consciousness is a process of events occurring in a wide, basic field of proto-conscious experience. These events, or “occasions of experience,” may be comparable to quantum state reductions, or actual events in physical reality (Shimony, 1993). This suggests that consciousness may involve quantum state reductions (e.g. a form of quantum computation).
But what of Whitehead’s basic field of proto-conscious experience? In what medium are the “occasions of experience” (quantum state reductions) occurring? Could proto-conscious qualia simply exist in the empty space of the universe?
What is empty space? Historically, empty space has been described as either an absolute void or a pattern of fundamental geometry. Democritus and the Michaelson-Morley results argued for “nothingness” while Aristotle (“plenum”) and Maxwell (“ether”) rejected the notion of emptiness in favor of “something”–a background pattern. Einstein weighed in on both sides of this debate, initially supporting the concept of a void with his theory of special relativity but then reversing himself in his theory of general relativity and its curved space and geometric distortions-the space-time metric. Could proto-conscious qualia be properties of the metric, fundamental space-time geometry?
What is fundamental space-time geometry? We know that at extremely small scales, space-time is not smooth, but granular, or quantized. This occurs at the infinitesimal Planck scale (10-33 cm, 10-43 secs). The fundamental level of spacetime geometry is described through quantum gravity. A final theory of quantum gravity could unite quantum theory and general relativity, the great divide in modern physics.
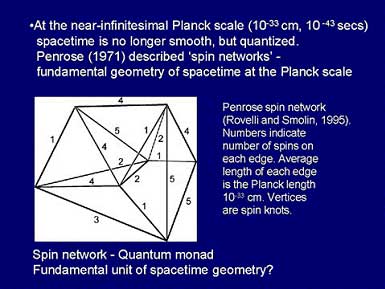
Figure 7. A spin network. Introduced by Roger Penrose (1971) as a quantum mechanical description of the geometry of space, spin networks describe spectra of discrete Planck scale volumes and configurations (with permission, Rovelli and Smolin, 1995).
At the basic level, this granularity has been modeled by Roger Penrose as a dynamic web of quantum spins. These “spin networks” create an array of geometric volumes and configurations at the Planck scale which dynamically evolve and define space-time geometry. Other approaches to this problem include “string theory ,” but regardless of which explanation best characterizes the fundamental level and the basis for quantum gravity, if panpsychist (or pan-protopsychist, or pan-experiential) philosophical approaches are correct, the fundamental level (Planck scale) the “funda-mental” level could provide the basis for qualia or proto-conscious experience. Further, if qualia are embedded at the Planck scale, then perhaps (as suggested by Roger Penrose) Platonic values like mathematical truth and aesthetic values are embedded there as well.
The Quantum Connection
If proto-conscious information and Platonic values are embedded at the Planck scale, how could they be linked to biology? How could our brains access, or be influenced by these infinitesimal features? A possible solution comes through quantum mechanics, or quantum theory.
Quantum theory describes the bizarre behavior of particles and energy at the scale of atoms and sub-atomic particles. A century of experimental observation of quantum systems have shown that, at least at small scales, particles (mass) can exist in two or more states or locations simultaneously (quantum superposition). But in our everyday world objects seem definite, and occupy single states and locations. The transition from quantum possibilities to definite, classical states is often called “collapse of the wave function,” or “quantum state reduction.”
Experimental evidence in the early part of this century led great theorists Bohr, Heisenberg and Wigner to conclude (the “Copenhagen interpretation”) that objects remain in wave-like quantum superposition until observed by a conscious human being–consciousness causes collapse of the wave function! To illustrate the apparent absurdity of this conclusion, in the 1930’s Schroedinger devised his famous thought experiment: “Schroedinger’s cat.” A living cat is placed in a box into which poison can be released by a quantum event, e.g., sending a photon through a half-silvered mirror. So there are equal possibilities that the cat is either dead or alive. As a quantum phenomenon, the photon is in superposition, and so both passes through, and does not pass through, the half silvered mirror. But according to the Copenhagen interpretation, until a conscious being opens the box to observe, the cat is both dead and alive. Schroedinger’s point was that the conscious observer interpretation was incorrect.
Other explanations have been developed. David Bohm’s theory avoids collapse (but raises other problems), and the “multiple worlds” view holds that each possibility in a superposition evolves into a new and separate universe. Modern physics describes environmental “decoherence,” essentially saying that any interaction between a quantum system and the outside world causes loss of the quantum superposition with random choice of particular classical states. However there is no explanation for the fate of quantum superpositions which remain isolated from environment.
Many physicists now believe that intermediate between tiny quantum-scale systems and “large” cat-size systems some objective factor disturbs the superposition to cause collapse, or “objective reduction (OR).” For example the GRW theory (after its proponents Ghirardi, Rimini and Weber) suggests that as a quantum superposition grows to a critical number of particles in superposition (~1017), the system spontaneously reduces to classical states. Experimental evidence has not supported GRW. According to Roger Penrose the objective factor causing reduction is an intrinsic feature of space-time itself (quantum gravity).
To begin, Penrose extends Einstein’s theory of general relativity (in which mass equates to curvature in space-time) down to the Planck scale. Quantum superposition–actual separation (displacement) of mass from itself– is equivalent to simultaneous spacetime curvatures in opposite directions, causing “bubbles,” or separations in fundamental reality. (To illustrate, 4-dimensional space-time is simplified as a 2 dimensional space-time sheet — Figure 8). The Penrose view is similar to the multiple worlds view in that superposition involves a separation in underlying reality, however rather than evolving an entire new universe, Penrose reasons that these bubble-like separations are unstable and reduce to specific states and locations after a critical degree of separation. Objective reductions are thus a self-organizing process at the fundamental level of reality. If proto-conscious experience is rooted in the Planck scale, then such self-organizing objective reductions are processes occurring in an experiential medium.
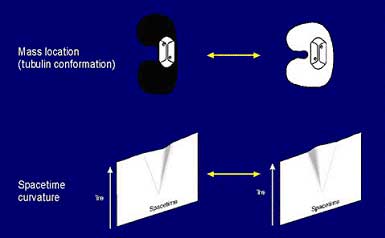
Figure 8. According to Einstein’s general relativity, mass is equivalent to curvature in spacetime geometry. Penrose applies this equivalence to the fundamental Planck scale. The motion of an object between two conformational states of a protein such as tubulin (top) is equivalent to two curvatures in spacetime geometry as represented as a two-dimensional spacetime sheet (bottom).
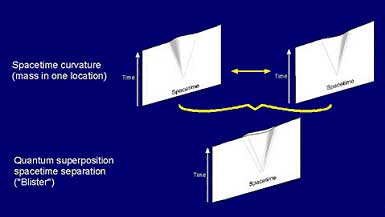
Figure 9. Spacetime superposition/separation bubble (bottom) will reduce, or collapse to one or the other spacetime curvatures (top).
Superposition and subsequent reduction, or collapse, to single, classical states may have profoundly important applications in technology
The critical threshold for Penrose quantum gravity OR is defined by the indeterminacy principle:
E = h/T
where E is the gravitational self-energy of the superposed mass separated from itself (the magnitude of the superposition), h is Planck’s constant divided by 2pi, and T is the coherence time until collapse occurs. Thus, the size and energy of a system in superposition, or the degree of space-time separation, is inversely related to the time T until reduction. (E can be calculated from the superposed mass m and the separation distance a. See e.g. Hameroff and Penrose, 1996a.)
Assuming isolation, the following masses in superposition would collapse at the designated times, according to Penrose’s objective reduction:
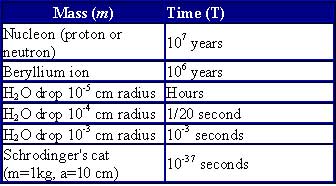
Other quantum features include quantum coherence, in which quantum particles may merge into unified objects, such as Bose-Einstein condensates. Also, quantum particles once united, when separated remain somehow connected, or “entangled,” even over great distances (nonlocality).
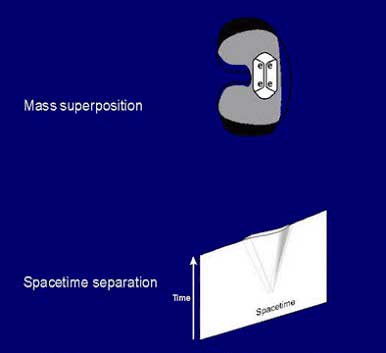
Figure 10. Mass superposition, e.g. a protein occupying two different conformational states simultaneously (top) is equivalent, according to Penrose, to simultaneous spacetime curvature in opposite directions – a separation, or bubble (“blister”) in fundamental spacetime geometry.
How can quantum state reduction by objective reduction and other quantum features help explain consciousness?
Quantum Computation
Superposition and subsequent reduction, or collapse, to single, classical states may have profoundly important applications in technology, as well as toward the understanding of consciousness. In the 1980s Benioff, Feynmann, Deutsch and other physicists proposed that quantum states could interact (via entanglement) and enact computation while in quantum superposition of all possible states (“quantum computing”).
Classical computing utilizes binary bits as either 1 or 0; quantum computations involve the processing of superpositioned “qubits” of both 1 and 0 (and other states) simultaneously.
Quantum theory also tells us that two or more particles, if once together, will remain somehow connected (“entangled”), even when separated by great distances. Qubits can interact by quantum entanglement, so that quantum computing is able to achieve a nearly infinite parallel computational ability. Quantum computers, if they can be constructed, will be able to solve important problems (e.g. searches, factoring large numbers) with efficiency unattainable in classical computers (Shor, 1994).
Researchers have developed a “Figure of Merit” M for proposed quantum computing technologies (Modified from Barenco, 1996 & DiVincenzo, 1995). M is related to the number of elementary operations performed per qubit before the superposition/computation is disrupted by decoherence (or in the case of microtubules in the Orch OR proposal, to be described below, before objective reduction terminates the superposition).
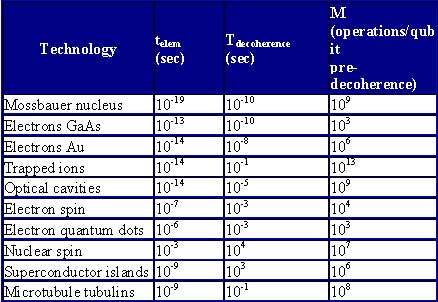
Results, or solutions in quantum computing are obtained when, after a period of quantum superposition/computation, the qubits “collapse,” or reduce to classical bit states (“collapse of the wave function”). As quantum superposition may only occur in isolation from environment, collapse (reduction) may be induced by breaching isolation (this is what is envisioned in technological quantum computers–making a measurement). But what about quantum superpositions which remain isolated, for example Schroedinger’s mythical cat which is both dead and alive? If the collapse occurs by Penrose OR, and if proto-conscious experience occurs at the fundamental level of reality, then such quantum computations could be conscious.
Could Penrose objective reduction occur in the brain? If so (from E = h/T) time T would be expected to coincide with known neurophysiological processes with time scales from tens to hundreds of milliseconds (e.g. 25 msec for coherent 40 Hz, 100 msec for alpha EEG, 500 msec for sensory threshold events such as Libet’s famous 1979 experiments). In what types of brain structures might quantum computation with objective reduction occur? For T in this range we can calculate (from E = h/T, and with E related to mass m as described in Hameroff and Penrose, 1996a) that superpositioned mass m in the nanogram range would be required for conscious events of 40 to 500 msec. What brain components in nanogram quantitites could support quantum computation and objective reduction? What is m?
Are Proteins Qubits?
Biological life is organized by proteins. By changing their conformational shape, proteins are able to perform a wide variety of functions, including muscle movement, molecular binding, enzyme catalysis, metabolism, and movement. Dynamical protein structure results from a “delicate balance among powerful countervailing forces” (Voet & Voet, 1995). The types of forces acting on proteins include charged interactions (such as covalent, ionic, electrostatic, and hydrogen bonds), hydrophobic interactions, and dipole interactions. The latter group, also known as van der Waals forces, encompasses three types of interactions:
- permanent dipole – permanent dipole,
- permanent dipole – induced dipole, and
- induced dipole – induced dipole (London dispersion forces)
As charged interactions cancel out, hydrophobic and dipole – dipole forces are left to regulate protein structure. While induced dipole – induced dipole interactions, or London dispersion forces, are the weakest of the forces, they are also the most numerous and influential. Indeed, they may be critical to protein function. For example, anesthetics are able to bind in hydrophobic “pockets” of certain neural proteins and ablate consciousness by virtue of disrupting these London forces. London force attraction between any two atoms is usually less than a few kilojoules; however, since thousands occur in each protein, they add up to thousands of kilojoules per mole, and cause changes in conformational structure. As London forces are instrumental in protein folding (a problem intractable to conventional computational simulation), protein conformation and folding may be quantum computations.
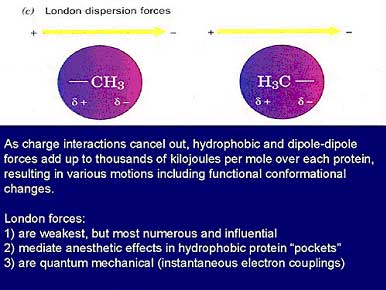
Figure 11. A type of van der Waals force, the London dispersion force, is quantum mechanical and governs both protein conformation.
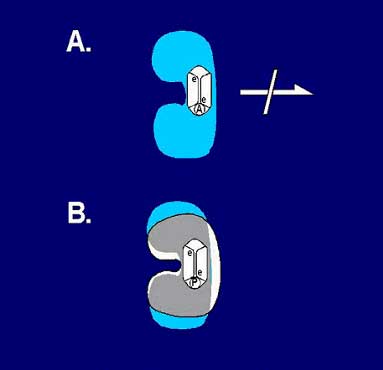
Figure 12. A. An anesthetic gas molecule (A) in a hydrophobic pocket of critical brain protein (receptors, channels, tubulin etc.) prevents normally occurring London forces, preventing protein conformational dynamics and superposition necessary for consciousness. B. A psychedelic hallucinogen (P) acts in hydrophobic pocket in critical brain protein to promote and sustain superposition, ‘expanding’ consciousness (see Figure 25).
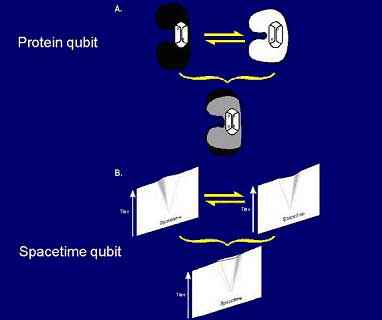
Figure 13. A. Protein qubit. A protein such as tubulin can exist in two conformations determined by quantum London forces in hydrophobic pocket (top), or superposition of both conformations (bottom). B. The protein qubit corresponds to two alternative spacetime curvatures (top), and superposition/separation (bubble) of both curvatures (bottom).
If proteins are qubits, arrays or assemblies of proteins in some type of organelle or biomolecular structure which could be isolated from environmental decoherence could be a quantum computer. Ideal structures would be:
- Abundant;
- Capable of information processing and computation;
- Functionally important (e.g., regulating synapses);
- Self-organizing;
- Tunable by input information (e.g., microtubule-associated protein orchestration);
- Periodic and crystal-like in structure (e.g., dipole lattice);
- Isolated (transiently) from environmental decoherence;
- Conformationally coupled to quantum events (e.g., London forces);
- Cylindrical wave-guide structure; and,
- Plasma-like charge layer coating.
While various structures/organelles have been suggested (e.g., membrane proteins, clathrins, myelin, pre-synaptic grids, and calcium ions), the most logical candidates are microtubule automata.
Microtubule Quantum Automata – The “Orch OR” Model
The Penrose-Hameroff model of “orchestrated objective reduction” (Orch OR) proposes that:
- Tubulin subunits within microtubules act as qubits, switching between states on a nanosecond (10-9 sec) scale governed by quantum London forces in hydrophobic pockets;
- Quantum superposition/computation occur in microtubule automata within brain neurons and glia;
- Tubulin qubits interact computationally by nonlocal quantum entanglement according to the Schroedinger equation;
- Quantum superposition/quantum computation of tubulin qubits corresponds with pre-conscious processes
- After time T, the pre-conscious quantum computation phase reaches OR threshold and “self-collapse” occurs which is an actual event in fundamental space-time geometry. This event selects a particular configuration of Planck-scale experiential geometry, enacting a “moment of awareness,” “occasion of experience” or conscious event.
- Quantum computations are “tuned,” or orchestrated by feedback from microtubule-associated proteins (MAPs) during classical phases which alternate with quantum phases (e.g. every 25 msec). Quantum states extend between and among neurons by gap junctions, windows between cells.
- The choice of states in the OR process is neither random, nor algorithmic, but (Penrose) “non-computable” meaning an influence by information embedded in Planck scale fundamental space-time geometry
- A sequence of OR events (e.g. at 40 Hz) provides a forward flow of subjective time and “stream” of consciousness;
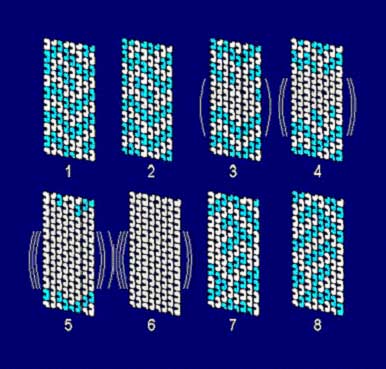
Figure 14. Microtubule automaton sequence simulation in which classical computing (step 1) leads to emergence of quantum coherent superposition (steps 2-6) in certain (gray) tubulins due to pattern resonance. Step 6 (in coherence with other microtubule tubulins) meets critical threshold related to quantum gravity for self-collapse (Orch OR). Consciousness (Orch OR) occurs in the step 6 to 7 transition. Step 7 represents the eigenstate of mass distribution of the collapse which evolves by classical computing automata to regulate neural function. Quantum coherence begins to re-emerge in step 8.
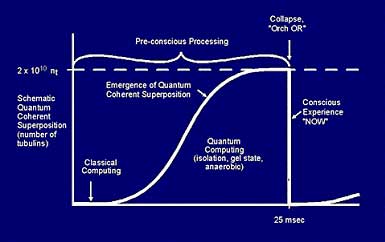
Figure 15. Schematic graph of proposed pre-conscious quantum superposition (number of tubulins) emerging versus time in microtubules. Area under curve connects superposed mass energy E with collapse time T in accordance with E=(h/T. E may be expressed as n, the number of tubulins whose mass separation (and separation of underlying space time) for time T will self-collapse. For T = 25 msec (e.g. 40 Hz oscillations), n = 2 x 10 tubulins.
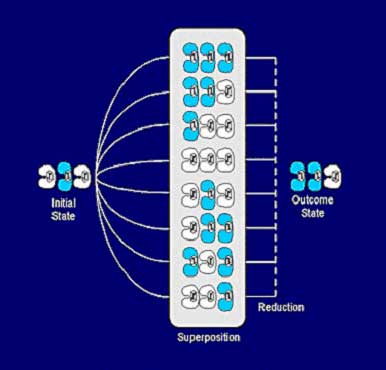
Figure 16. Schematic of quantum computation of three tubulins which begin (left) in initial classical states, then enter isolated quantum superposition in which all possible states coexist. After reduction, one particular classical outcome state is chosen (right).
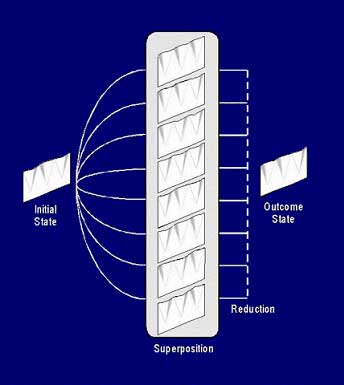
Figure 17. Schematic quantum computation in spacetime curvature for three mass distributions (e.g. tubulin conformations in Figure 23) which begin (left) in initial classical states, then enter isolated quantum superposition in which all possible states coexist. After reduction, one particular classical outcome state is chosen (right).
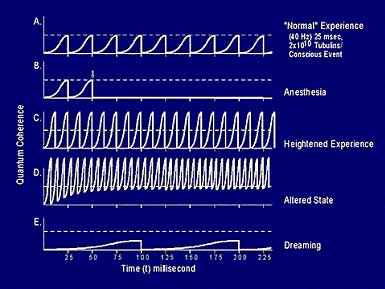
Figure 18. Quantum superposition/entanglement in microtubules for 5 states related to consciousness. Area under each curve equivalent in all cases. A. Normal 30 Hz experience: as in Figure 22. B. Anesthesia: anesthetics bind in hydrophobic pockets and prevent quantum delocalizability and coherent superposition. C. Heightened Experience: increased sensory experience input (for example) increases rate of emergence of quantum superposition. Orch OR threshold is reached faster, and Orch OR frequency increases. D. Altered State: even greater rate of emergence of quantum superposition due to sensory input and other factors promoting quantum state (e.g. meditation, psychedelic drug etc.). Predisposition to quantum state results in baseline shift and collapse so that conscious experience merges with normally sub-conscious quantum computing mode. E. Dreaming: prolonged sub-threshold quantum superposition time.
- At the nanoscale each event determines new classical states of microtubule automata which regulate synaptic and other neural functions;
- During the pre-conscious quantum superposition/computation phase, oscillations are “tuned” and “orchestrated” by microtubule-associated proteins (MAPs), providing a feedback loop between the biological system and the quantum state (hence Orch OR);
- Quantum states in microtubules may link to those in microtubules in other neurons and glia by tunneling through gap junctions, permitting extension of the quantum state throughout significant volumes of the brain.
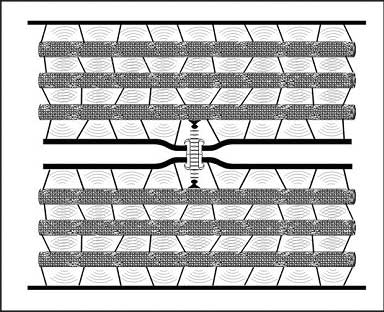
Figure 19. Schematic representation of a gap junction connecting two dendrites in which microtubules are in quantum superposition/quantum computation “tuned” by interconnecting MAP proteins as suggested in the Penrose-Hameroff Orch OR model. On either side of the gap junction, dendritic lamellar bodies (DLBs) containing mitochondria may act as tunneling diodes to convey the quantum state between the dendrites. (orchestrated objective reduction: Orch OR). Gap junctions may enable quantum tunneling among dendrites resulting in macroscopic quantum states.
- From E = h/T we can calculate the size and extension of Orch OR events which correlate with subjective or neurophysiological descriptions of conscious events.

Orch OR, Cognition and Free Will
Quantum computation with objective reduction (Orch OR) is potentially applicable to cognitive activities. While classical neural-level computation can provide a partial explanation, the Orch OR model allows far greater information capacity, and addresses issues of conscious experience, binding, and non-computability consistent with free will. Functions like face recognition and volitional choice may require a series of conscious events arriving at intermediate solutions. For the purpose of illustration consider single Orch OR events in these two types of cognitive activities.
Imagine you briefly see a familiar woman’s face. Is she Amy, Betty, or Carol? Possibilities may superpose in a quantum computation. For example, during 25 milliseconds of pre-conscious processing, quantum computation occurs with information (Amy, Betty, Carol) in the form of “qubits,” superposed states of microtubule tubulin subunits within groups of neurons. All possibilities coexist. As threshold for objective reduction is reached, an instantaneous conscious event occurs. The superposed tubulin qubits reduce to definite states, becoming bits, and one particular possibility is chosen. Now, you recognize that she is Carol! (an immense number of possibilities could be superposed in a human brain’s 1019 tubulins).
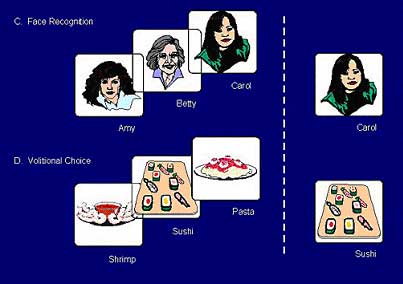
Figure 20. Face recognition. A familiar face induces superposition (left) of three possible solutions (Amy, Betty, Carol) which “collapse” to the correct answer Carol (right). Volitional choice. Three possible dinner selections (shrimp, sushi, pasta) are considered in superposition (left), and collapse via Orch OR to choice of sushi (right).
In a volitional act possible choices may be superposed. Suppose for example you are selecting dinner from a menu. During pre-conscious processing, shrimp, sushi and pasta are superposed in a quantum computation. As threshold for objective reduction is reached, the quantum state reduces to a single classical state. A choice is made. You’ll have sushi!
How does the choice actually occur? In a conventional neural network scheme, the selection criteria can be described by a deterministic algorithm which precludes the possibility of free will. The non-computable influence in Orch OR may be useful in understanding free will.
The problem in understanding free will is that our actions seem neither totally deterministic nor random (probabilistic). What else is there in nature? As previously described, in OR (and Orch OR) the reduction outcomes are neither deterministic nor probabilistic, but involve a factor which is “non-computable.” The microtubule quantum superposition evolves linearly (analogous to a quantum computer) but is influenced at the instant of collapse by hidden non-local variables (quantum-mathematical logic inherent in fundamental spacetime geometry). The possible outcomes are limited, or probabilities set (“orchestrated”), by neurobiological feedback (in particular microtubule associated proteins, or MAPs). The precise outcome3/4our free will actions3/4are chosen by effects of the hidden logic on the quantum system poised at the edge of objective reduction.
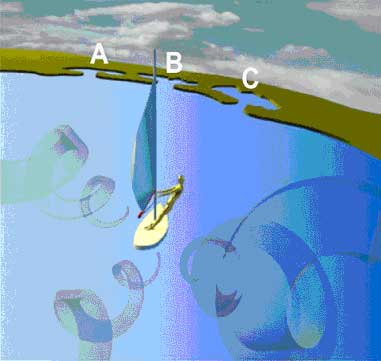
Figure 21. Free will may be seen as the result of deterministic processes (behavior of trained robot windsurfer) acted on repeatedly by non-computable influences, here represented as a seemingly capricious wind.
Consider a sailboard analogy for free will. A sailor sets the sail in a certain way; the direction the board sails is determined by the action of the wind on the sail. Let’s pretend the sailor is a non-conscious robot zombie run by a quantum computer which is trained and programmed to sail. Setting and adjusting of the sail, sensing the wind and position, jibing and tacking (turning the board) are algorithmic and deterministic, and may be analogous to the pre-conscious, quantum computing phase of Orch OR. The direction and intensity of the wind (seemingly capricious, or unpredictable) may be considered analogous to Planck scale hidden non-local variables (e.g. “Platonic” quantum-mathematical logic inherent in space-time geometry). The choice, or outcome (the direction the boat sails, the point on shore it lands) depends on the deterministic sail settings acted on repeatedly by the apparently unpredictable wind. Our “free will” actions could be the net result of deterministic processes acted on by hidden quantum logic at each Orch OR event. This can explain why we generally do things in an orderly, deterministic fashion, but occasionally our actions or thoughts are surprising, even to ourselves.
Biological Feasibility–the Problem of Decoherence
Orch OR and other quantum approaches can in principle explain enigmatic features of consciousness. But how could delicate quantum superposition/computation be isolated from environmental decoherence in the brain (generally considered to be a noisy thermal bath) while also communicating (input/output) with the environment? One possibility is that quantum superposition/computation occurs in an isolation phase which alternates with a communicative phase, for example at 40 Hz. One of the most primitive biological functions is the transition of cytoplasm between a liquid, solution (“sol”) phase, and a solid, gelatinous (“gel”) phase due to assembly and disassembly of the cytoskeletal protein actin. Actin sol-gel transitions can occur at 40 Hz or faster, and are known to be involved in neuronal synaptic release mechanisms.
Mechanisms for enabling microtubule quantum computation and avoiding decoherence long enough to reach threshold may include (for details see Hagan et al, 2000):
- Sol-gel transitions;
- Plasma phase sleeves (microtubules are surrounded by counterion zones (Sackett);
- Hydrophobic pockets;
- Hollow microtubule cores;
- Laser-like pumping, including environment (Frohlich, Conrad).
- Topological quantum error correcting codes
Another apparent obstacle to the Orch OR proposal is how the weak energy involved in the gravitational collapse can be influential. For a detailed description of this problem and potential solutions, see Hameroff, 1998c. One possibility is that the gravitational self-energy is delivered to the involved tubulins via London forces virtually instantaneously (e.g. within one Planck time) so that the power (energy/time) is significant–approximately one kilowatt per tubulin per Orch OR event.
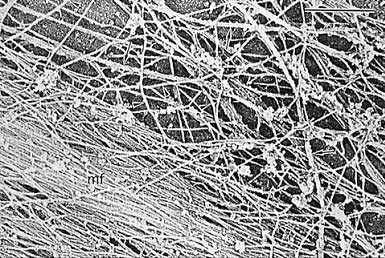
Figure 22. Immunoelectron micrograph of cytoplasm showing microtubules (arrows), intermediate filaments (arrowheads) and actin microfilaments (mf). Dense gel of actin (lower left) completely obscures (?isolates) microtubules. Actin sol-gel transitions can occur at 40 Hz or faster. Scale bar (upper right): 500 nanometers. With permission from Svitkina et al, 1995.
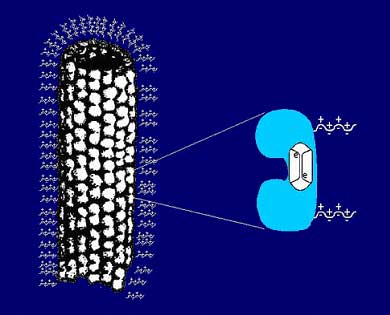
Figure 23. Dan Sackett at NIH recently described a plasma-like sleeve of charged ions surrounding microtubules at precisely optimal pH. Quantum excitations/ordering of surrounding water (Jibu/Yasue/Hagan)
Consciousness and Evolution
When in the course of evolution did consciousness first appear? Are all living organisms conscious, or did consciousness emerge more recently, e.g. with language or toolmaking? Or did consciousness appear somewhere in between, and if so, when and why? The Orch OR model (unlike other models of consciousness) is able to make a prediction as to the onset of consciousness. Based on E = h/T we can ask, for example, is it feasible for single cell organisms such as paramecium (which exhibit complex behavior such as graceful swimming, mating and learning) to be conscious? Single cells including paramecium should contain approximately 107 tubulins, so T would be 50,000 msec, or nearly one minute. This seems unlikely. Larger organisms such as the nematode worm (e.g., C. elegans) with 300 neurons (3 x 109 tubulins) would need to maintain quantum isolation for only 133 msec – not unreasonable. Such organisms (tiny worms and urchins) were prevalent at the beginning of the “Cambrian explosion,” a burst of evolution which occurred 540 million years ago. Did primitive consciousness (via Orch OR) accelerate evolution and precipitate the Cambrian explosion?
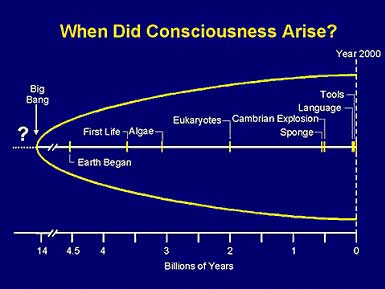
Figure 24. A time-line of when consciousness could have arisen.
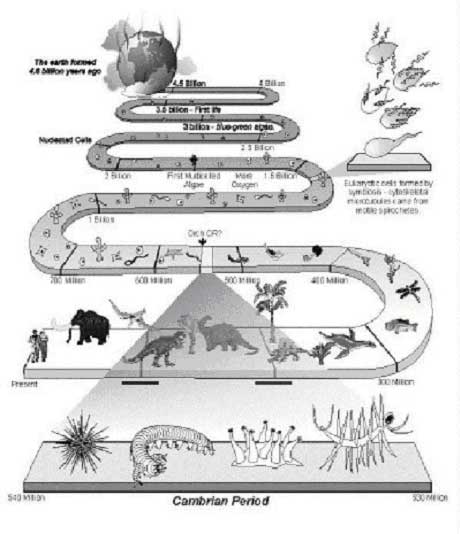
Figure 25. Organisms present at the early Cambrian explosion (e.g. tiny urchins, worms and suctorians) are the right size for primitive consciousness by Orch OR.

Figure 26. Actinosphaerium is a tiny urchin like those present at the early Cambrian explosion. Each has about one hundred rigid axonemes about 300 microns long, made up of a total of about 3 x 10 tubulins (with permission from L.E. Roth).

Figure 27. Cross-section of single axoneme of actinosphaerium – a double spiral array of interconnected microtubules. Scale bar: 500 nm (with permission from L.E. Roth).
Would consciousness be advantageous to survival (above and beyond intelligent, complex behavior)? It seems that, yes, consciousness would indeed be advantageous to survival, and hence capable of accelerating evolution. Non-computable behavior (unpredictability, intuitive actions) would be beneficial in predator-prey relations. Having conscious experience of taste would promote finding food; the experience of pain would promote avoiding predators. And the pleasurable qualia of sex would promote reproduction.
So “what is it like to be a worm?” Lacking our sensory apparatus, associative memory and complex nervous system such primitive consciousness would be a mere glimmer, a disjointed smudge of reality. But qualitatively, at a basic level, such primitive consciousness would be akin to ours.
What about future evolution? Will consciousness occur in computers? The advent of quantum computers opens the possibility, however as presently envisioned quantum computers will have insufficient mass in superposition (e.g. electrons) to reach threshold for objective reduction. Instead, superpositions will be disrupted by environmental decoherence. Conceivably, future generations of quantum computers could satisfy requirements for objective reduction and consciousness.
Conclusions
- Brain processes relevant to consciousness extend downward within neurons to the level of cytoskeletal microtubules
- Both classical and quantum computation in microtubules within neurons may be necessary for consciousness
- An explanation for conscious experience requires (in addition to neuroscience and psychology) a modern form of pan-protopsychism in which proto-conscious qualia are embedded in the basic level of reality, as described by modern physics
- Roger Penrose’s physics of objective reduction (OR) connects brain structures to fundamental reality, leading to the Penrose-Hameroff model of quantum computation with objective reduction in microtubules (orchestrated objective reduction: Orch OR)
- The Orch OR model is consistent with known neurophysiological processes, generates testable predictions, and is the type of fundamental, multi-level, interdisciplinary theory which may account for the mind’s enigmatic features
References
References in the text may be found in the following “Orch OR” papers. See also http://www.consciousness.arizona.edu/hameroff .
Penrose, R. (1989) The Emperor’s New Mind, Oxford Press, Oxford, U.K
Penrose, R. (1994) Shadows of the Mind, Oxford Press, Oxford, U.K.
Penrose, R., Hameroff, S.R. (1995) What gaps? Reply to Grush and Churchland. Journal of Consciousness Studies 2(2):99-112.
Hameroff, S.R., and Penrose, R., (1996a) Orchestrated reduction of quantum coherence in brain microtubules: A model for consciousness. In: Toward a Science of Consciousness – The First Tucson Discussions and Debates, S.R. Hameroff, A. Kaszniak and A.C. Scott (eds.), MIT Press, Cambridge, MA.pp. 507-540. Also published in Mathematics and Computers in Simulation 40:453-480.
Hameroff, S.R., and Penrose, R. (1996b) Conscious events as orchestrated spacetime selections. Journal of Consciousness Studies 3(1):36-53.
Penrose, R. (1996) On gravity’s role in quantum state reduction. General relativity and gravitation. 28(5): 581-600
Penrose, R. (1997) On understanding understanding. International Studies in the Philosophy of Science 11(1):7-20.
Penrose R. (1998) The large, the small, and the human mind Hameroff, S. (1998a) Did consciousness cause the Cambrian evolutionary explosion? In: Toward a Science of Consciousness II – The Second Tucson Discussions and Debates. Eds S Hameroff, A Kaszniak, A Scott
Hameroff, S. (1998f) Anesthesia, consciousness and hydrophobic pockets – A unitary quantum hypothesis of anesthetic action. Toxicology Letters 100/101-31-39. Also see. MIT Press, Cambridge MA pp 421-437
Hameroff, S. (1998b) “More neural than thou”: Reply to Churchland’s “Brainshy” in: Toward a Science of Consciousness II – The Second Tucson Discussions and Debates. Eds S Hameroff, A Kaszniak, A Scott. MIT Press, Cambridge MA pp 197-213
Hameroff, S. (1998c) Funda-mental geometry: The Penrose-Hameroff Orch OR model of consciousness. In: The geometric universe – Science, geometry and the work of Roger Penrose. Eds. S.A. Huggett, L.J. Mason, K.P. Tod, S.T. Tsou, and N.M.J. Woodhouse. Oxford Press, Oxford, U.K. pp 135-160