More-realistic 3D imaging technique speeds up production of movie images, modeling human organs
November 22, 2013
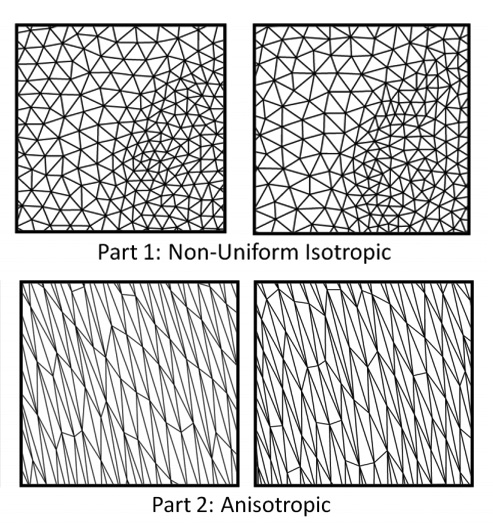
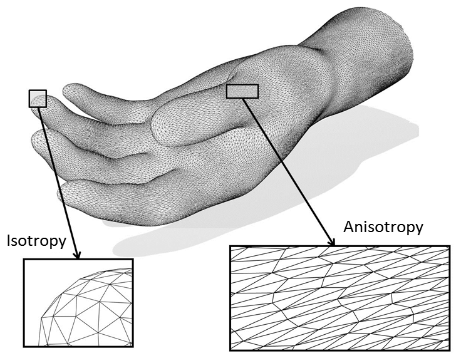
Guo and his team found that replacing isotropic triangles (part 1) with anisotropic triangles (part 2) in the particle-based method of creating images resulted in smoother representations of objects (credit: UT Dallas)
UT Dallas computer scientists have developed a technique to make 3D images faster and with more accuracy.
The method uses anisotropic (irregular) triangles — triangles with sides that vary in length depending on their direction — to create 3D “mesh” computer graphics that more accurately approximate the shapes of the original objects, and in a shorter amount of time than current techniques.
These types of images are used in movies, video games and computer modeling of various phenomena, such as the flow of water or air across the Earth, the deformation and wrinkles of clothes on the human body, or in mechanical and other types of engineering designs.
Researchers hope this technique will also lead to greater accuracy in models of human organs to more effectively treat human diseases, such as cancer.
“Anisotropic mesh can provide better simulation results for certain types of problems, for example, in fluid dynamics,” said Dr. Xiaohu Guo, associate professor of computer science in the Erik Jonsson School of Engineering and Computer Science whose team created the technique.
The technique finds a practical application of the Nash embedding theorem, which was named after mathematician John Forbes Nash Jr., subject of the film A Beautiful Mind.
How to generate an image up to 125 times faster
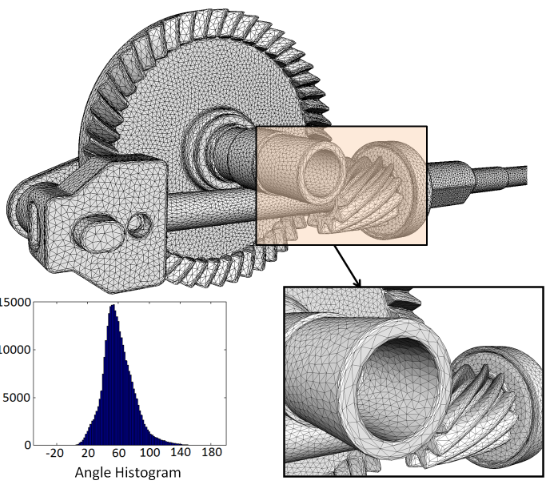
The computer graphics field represents shapes in the virtual world through triangle mesh. Traditionally, it is believed that isotropic triangles — where each side of the triangle has the same length regardless of direction — are the best representation of shapes.
However, the aggregate of these uniform triangles can create edges or bumps that are not on the original objects. Because triangle sides can differ in anisotrophic images, creating images with this technique would allow the user flexibility to more accurately represent object edges or folds.
Guo and his team found that replacing isotropic triangles with anisotropic triangles in the particle-based method of creating images resulted in smoother representations of objects. Depending on the curvature of the objects, the technique can generate the image up to 125 times faster than common approaches.
For example, 155 seconds to create a circular image with Guo’s approach, versus more than 19,500 seconds for a common approach to generate an image of similar quality.
Objects using anisotropic triangles are of a more accurate quality, and most noticeable to the human eye when it comes to wrinkles and movement of clothes on human representatives.
Modeling organs
The next step of this research is moving from representing the surface of 3D objects to representing 3D volume. “If we are going to create accurate representations of human organs, we need to account for the movement of cells below the organ’s surface,” Guo said.
Zichun Zhong, research assistant in computer science and PhD candidate at UT Dallas, was also involved in this research. Researchers from the University of Hong Kong, Inria Nancy Grand Est in France, Nvidia Corporation in California and UT Southwestern Medical Center also participated.
“These types of images are used in movies, video games, Computer-Aided Design (CAD), Computer-Aided Manufacturing (CAM), computational fluid dynamics (CFD) fields, scientific visualization, architecture design, etc.,” Zhong explained to KurzweilAI.
“It can work better to capture the behavior of physical phenomena, such as such as the flow of water or air across the Earth, the deformation and wrinkles of clothes on the human body, or in mechanical and other types of engineering designs. Medical scientists hope this technique will also lead to greater accuracy in models of human organs to more effectively treat human diseases, such as cancer.
“If we can find good commercial partners and attractive applications, it will appear on the market within several months.”
Abstract of SIGGRAPH 2013 presentation
This paper introduces a particle-based approach for anisotropic sur- face meshing. Given an input polygonal mesh endowed with a Rie- mannian metric and a specified number of vertices, the method generates a metric-adapted mesh. The main idea consists of mapping the anisotropic space into a higher dimensional isotropic one, called “embedding space”. The vertices of the mesh are generated by uniformly sampling the surface in this higher dimensional embedding space, and the sampling is further regularized by optimizing an energy function with a quasi-Newton algorithm. All the computations can be re-expressed in terms of the dot product in the embedding space, and the Jacobian matrices of the mappings that connect different spaces. This transform makes it unnecessary to explicitly represent the coordinates in the embedding space, and also provides all necessary expressions of energy and forces for efficient computations. Through energy optimization, it naturally leads to the desired anisotropic particle distributions in the original space. The triangles are then generated by computing the Restricted Anisotropic Voronoi Diagram and its dual Delaunay triangulation. We compare our results qualitatively and quantitatively with the state-of-the-art in anisotropic surface meshing on several examples, using the standard measurement criteria.