Do our brains use the same kind of deep-learning algorithms used in AI?
February 23, 2018
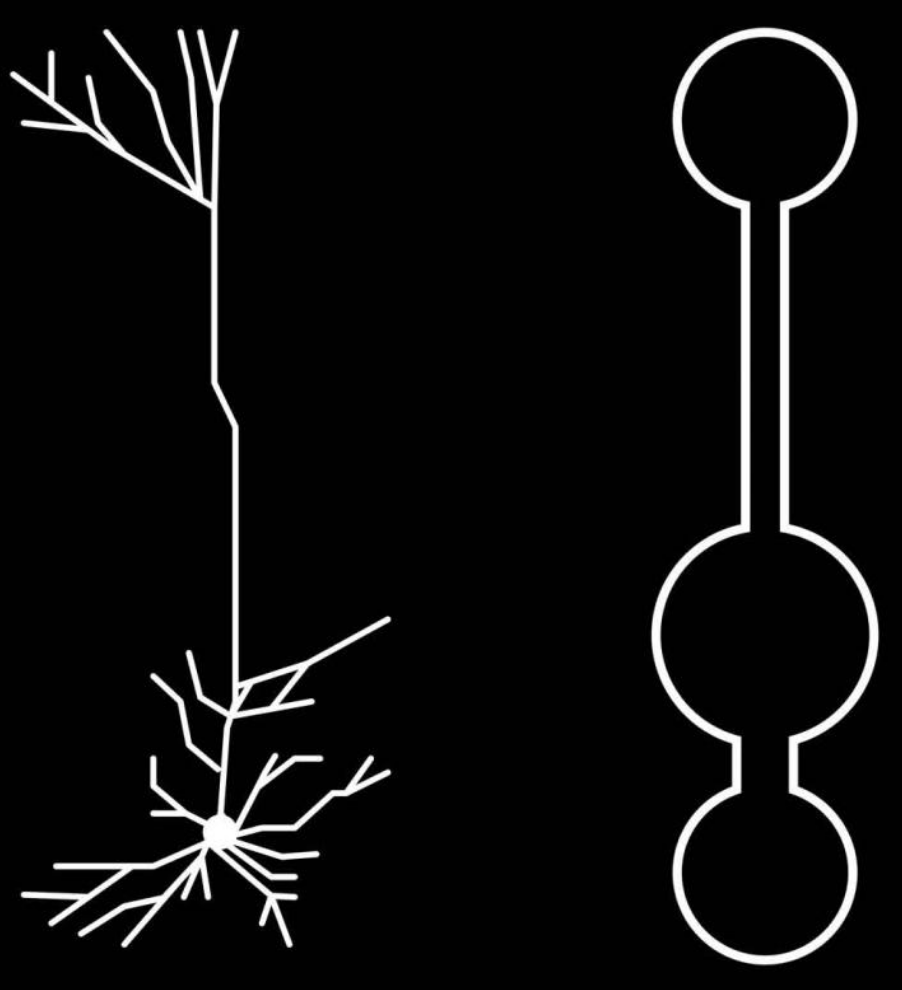
This is an illustration of a multi-compartment neural network model for deep learning. Left: Reconstruction of pyramidal neurons from mouse primary visual cortex, the most prevalent cell type in the cortex. The tree-like form separates “roots,” where bottoms of cortical neurons are located just where they need to be to receive signals about sensory input, from “branches” at the top, which are well placed to receive feedback error signals. Right: Illustration of simplified pyramidal neuron models. (credit: CIFAR)
Deep-learning researchers have found that certain neurons in the brain have shape and electrical properties that appear to be well-suited for “deep learning” — the kind of machine-intelligence used in beating humans at Go and Chess.
Canadian Institute For Advanced Research (CIFAR) Fellow Blake Richards and his colleagues — Jordan Guerguiev at the University of Toronto, Scarborough, and Timothy Lillicrap at Google DeepMind — developed an algorithm that simulates how a deep-learning network could work in our brains. It represents a biologically realistic way by which real brains could do deep learning.*
The finding is detailed in a study published December 5th in the open-access journal eLife. (The paper is highly technical; Adam Shai of Stanford University and Matthew E. Larkum of Humboldt University, Germany wrote a more accessible paper summarizing the ideas, published in the same eLife issue.)
Seeing the trees and the forest
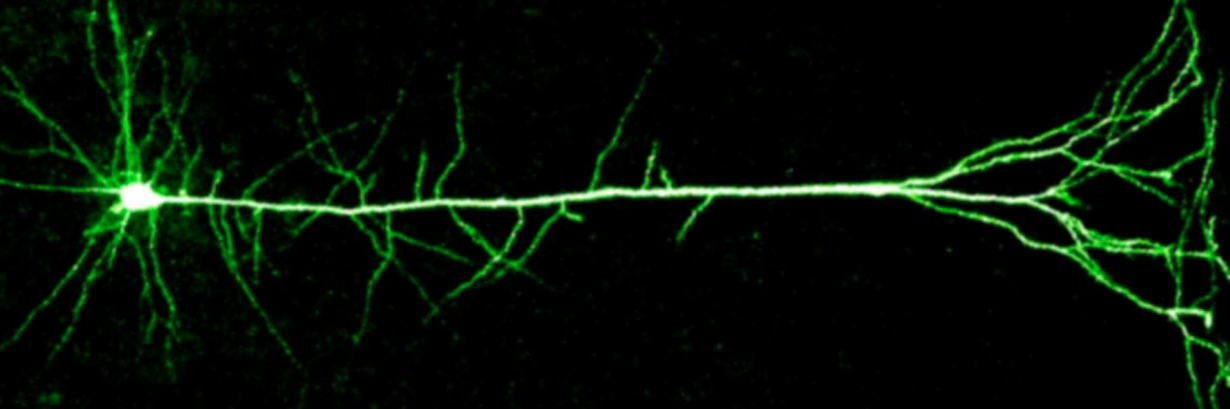
Image of a neuron recorded in Blake Richard’s lab (credit: Blake Richards)
“Most of these neurons are shaped like trees, with ‘roots’ deep in the brain and ‘branches’ close to the surface,” says Richards. “What’s interesting is that these roots receive a different set of inputs than the branches that are way up at the top of the tree.” That allows these functions to have the required separation.
Using this knowledge of the neurons’ structure, the researchers built a computer model using the same shapes, with received signals in specific sections. It turns out that these sections allowed simulated neurons in different layers to collaborate — achieving deep learning.
“It’s just a set of simulations so it can’t tell us exactly what our brains are doing, but it does suggest enough to warrant further experimental examination if our own brains may use the same sort of algorithms that they use in AI,” Richards says.
“No one has tested our predictions yet,” he told KurzweilAI. “But, there’s a new preprint that builds on what we were proposing in a nice way from Walter Senn‘s group, and which includes some results on unsupervised learning (Yoshua [Bengio] mentions this work in his talk).
How the brain achieves deep learning
The tree-like pyramidal neocortex neurons are only one of many types of cells in the brain. Richards says future research should model different brain cells and examine how they interact together to achieve deep learning. In the long term, he hopes researchers can overcome major challenges, such as how to learn through experience without receiving feedback or to solve the “credit assignment problem.”**
Deep learning has brought about machines that can “see” the world more like humans can, and recognize language. But does the brain actually learn this way? The answer has the potential to create more powerful artificial intelligence and unlock the mysteries of human intelligence, he believes.
“What we might see in the next decade or so is a real virtuous cycle of research between neuroscience and AI, where neuroscience discoveries help us to develop new AI and AI can help us interpret and understand our experimental data in neuroscience,” Richards says.
Perhaps this kind of research could one day also address future ethical and other human-machine-collaboration issues — including merger, as Elon Musk and Ray Kurzweil have proposed, to achieve a “soft takeoff” in the emergence of superintelligence.
* This research idea goes back to AI pioneers Geoffrey Hinton, a CIFAR Distinguished Fellow and founder of the Learning in Machines & Brains program, and program Co-Director Yoshua Bengio, who was one of the main motivations for founding the program. These researchers sought not only to develop artificial intelligence, but also to understand how the human brain learns, says Richards.
In the early 2000s, Richards and Lillicrap took a course with Hinton at the University of Toronto and were convinced deep learning models were capturing “something real” about how human brains work. At the time, there were several challenges to testing that idea. Firstly, it wasn’t clear that deep learning could achieve human-level skill. Secondly, the algorithms violated biological facts proven by neuroscientists.
The paper builds on research from Bengio’s lab on a more biologically plausible way to train neural nets and an algorithm developed by Lillicrap that further relaxes some of the rules for training neural nets. The paper also incorporates research from Matthew Larkam on the structure of neurons in the neocortex.
By combining neurological insights with existing algorithms, Richards’ team was able to create a better and more realistic algorithm for simulating learning in the brain.
The study was funded by the Natural Sciences and Engineering Research Council of Canada (NSERC), a Google Faculty Research Award, and CIFAR.
** In the paper, the authors note that a large gap exists between deep learning in AI and our current understanding of learning and memory in neuroscience. “In particular, unlike deep learning researchers, neuroscientists do not yet have a solution to the ‘credit assignment problem’ (Rumelhart et al., 1986; Lillicrap et al., 2016; Bengio et al., 2015). Learning to optimize some behavioral or cognitive function requires a method for assigning ‘credit’ (or ‘blame’) to neurons for their contribution to the final behavioral output (LeCun et al., 2015; Bengio et al., 2015). The credit assignment problem refers to the fact that assigning credit in multi-layer networks is difficult, since the behavioral impact of neurons in early layers of a network depends on the downstream synaptic connections.” The authors go on to suggest a solution.