‘Primitive’ quantum computer outperforms classical computers
May 13, 2016

A simulation of Brownian motion (random walk) of a dust particle (yellow) that collides with a large set of smaller particles (molecules of a gas) moving with different velocities in different random directions (credit: Lookang et al./CC)
Researchers at the Universities of Bristol and Western Australia have demonstrated a practical use of a “primitive” quantum computer, using an algorithm known as “quantum walk.” They showed that a two-qubit photonics quantum processor can outperform classical computers for this type of algorithm, without requiring more sophisticated quantum computers, such as IBM’s five-qubits cloud-based quantum processor (see IBM makes quantum computing available free on IBM Cloud).
Quantum walk is the quantum-mechanical analog of “random-walk” models such as Brownian motion (for example, the random motion of a dust particle in air). The researchers implemented “continuous-time quantum walk” computations on circulant graphs* in a proof-of-principle experiment.

The probability distribution of quantum walk on an example circulant graph. Sampling this probability distribution is generally hard for a classical computer, but simple on a primitive quantum computer. (credit: University of Bristol)
Jonathan Matthews, PhD., EPSRC Early Career Fellow and Lecturer in the School of Physics and the Centre for Quantum Photonics, explained in an open-access paper in Nature Communications: “An exciting outcome of our work is that we may have found a new example of quantum walk physics that we can observe with a primitive quantum computer, that otherwise a classical computer could not see. These otherwise hidden properties have practical use, perhaps in helping to design more sophisticated quantum computers.”
Microsoft | Quantum Computing 101
* A circulant graph is a graph where every vertex is connected to the same set of relative vertices, as explained in an open-access paper by Salisbury University student Shealyn Tucker, including a practical example of the use of a circulant graph:
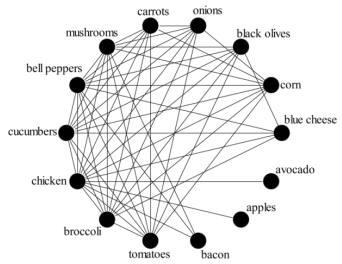
Example of a circulent graph depicting how products should be optimally collocated based on which products customers buy at a grocery store (credit: Shealyn Tucker/Salisbury University)
Abstract of Efficient quantum walk on a quantum processor
The random walk formalism is used across a wide range of applications, from modelling share prices to predicting population genetics. Likewise, quantum walks have shown much potential as a framework for developing new quantum algorithms. Here we present explicit efficient quantum circuits for implementing continuous-time quantum walks on the circulant class of graphs. These circuits allow us to sample from the output probability distributions of quantum walks on circulant graphs efficiently. We also show that solving the same sampling problem for arbitrary circulant quantum circuits is intractable for a classical computer, assuming conjectures from computational complexity theory. This is a new link between continuous-time quantum walks and computational complexity theory and it indicates a family of tasks that could ultimately demonstrate quantum supremacy over classical computers. As a proof of principle, we experimentally implement the proposed quantum circuit on an example circulant graph using a two-qubit photonics quantum processor.