This simple optoelectronic computer could one day outperform supercomputers for complex problems
November 15, 2016

Stanford post-doctoral scholar Peter McMahon, left, and visiting researcher Alireza Marandi examine a prototype of a new type of light-based computer. (credit: L.A. Cicero)
Stanford researchers have designed a new type of computer that combines optical and electronic technology to solve combinatorial optimization problems, which are challenging for traditional computers, even for supercomputers.
An optimal traveling salesman route through some U.S. capital cities (credit: SAS)
An example is the “traveling salesman” problem, in which a salesman has to visit a specific set of cities, each only once, and return to the first city, taking the most efficient route possible. The number of possible routes increases extremely rapidly as cities are added, and this underlies why the problem is difficult to solve.
Other examples of such problems include finding the optimal path for delivery trucks, minimizing interference in wireless networks, and determining how proteins fold. Even small improvements in some of these areas could result in massive monetary savings.
Quantum computers are also being explored to solve such problems, but “providing dense connectivity between qubits remains a major challenge,” the authors note in a paper published Oct. 20 in the journal Science.
The Stanford team has built an “Ising machine,” named for a mathematical model of magnetism. But instead of using magnetism, the team built an entirely new type of computer that blends optical and electrical processing.*
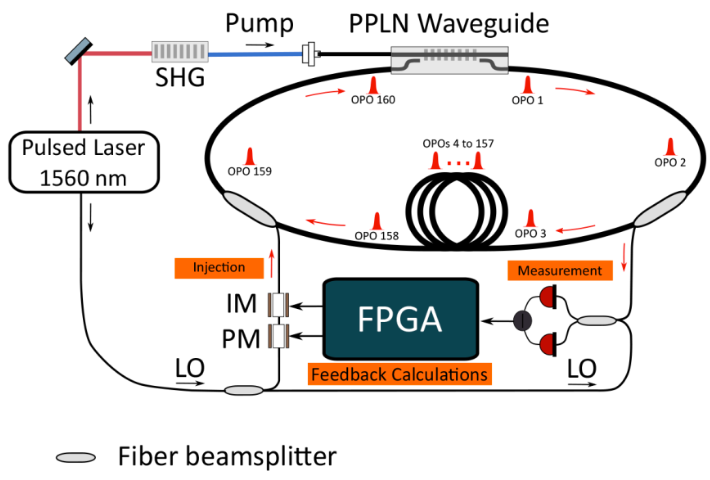
Experimental schematic of a measurement-feedback-based coherent Ising machine.
A time-division-multiplexed pulsed degenerate optical parametric oscillator is formed by a nonlinear crystal (PPLN) in a fiber ring cavity containing 160 pulses. A fraction of each pulse is measured and used to compute a feedback signal that effectively
couples the otherwise-independent pulses in the cavity. IM: intensity modulator; PM:
phase modulator; LO: local oscillator; SHG: second-harmonic generation; FPGA: field-programmable gate array. (credit: Peter L. McMahon et al./Science)
The team used a special kind of laser system, known as a “degenerate optical parametric oscillator.” When turned on, it will represent an upward- or downward-pointing “spin” in the classic Ising machine. Pulses of the laser represent a city’s position in a path the salesman could take.
Scaling up
If it can be scaled up, this non-traditional computer could save costs by finding more optimal solutions to problems that have an incredibly high number of possible solutions, the researchers suggest.
Nearly all of the materials used to make this machine are off-the-shelf elements that are already used for telecommunications. That, in combination with the simplicity of the programming, makes it easy to scale up, the researchers say. Stanford’s machine is currently able to solve 100-variable problems with any arbitrary set of connections between variables, and it has been tested on thousands of scenarios.
A group at NTT in Japan that consulted with Stanford’s team has also created an independent version of the machine; its study has been published alongside Stanford’s by Science.
For now, the Ising machine-based system still falls short of beating the processing power of traditional digital computers when it comes to combinatorial optimization.
Researchers from the National Institute of Informatics (Japan), University of Tokyo, NTT Basic Research Laboratories, and the ImPACT Program were also co-authors. This research was funded by the Impulsing Paradigm Change through Disruptive Technologies (ImPACT) Program of the Council of Science, Technology and Innovation (Cabinet Office, Government of Japan).
* A theoretical Ising machine acts like a reprogrammable network of artificial magnets, where each magnet only points up or down and, like a real magnetic system, it is expected to tend toward operating at low energy.
The theory is that, if the connections among a network of magnets can be programmed to represent the problem at hand, once they settle on the optimal, low-energy directions they should face, the solution can be derived from their final state. In the case of the traveling salesman, each artificial magnet in the Ising machine represents the position of a city in a particular path.
In an earlier version of this machine (published two years ago), the team members extracted a small portion of each pulse, delayed it and added a controlled amount of that portion to the subsequent pulses. In traveling salesman terms, this is how they program the machine with the connections and distances between the cities. The pulse-to-pulse couplings constitute the programming of the problem. Then the machine is turned on to try to find a solution, which can be obtained by measuring the final output phases of the pulses.
The problem in this previous approach was connecting large numbers of pulses in arbitrarily complex ways. It was doable but required an added controllable optical delay for each pulse, which was costly and difficult to implement.
The new Stanford Ising machine shows that a more affordable and practical version could be made by replacing the controllable optical delays with a digital electronic circuit, which emulates the optical connections among the pulses to program the problem.
Abstract of A fully-programmable 100-spin coherent Ising machine with all-to-all connections
Unconventional, special-purpose machines may aid in accelerating the solution of some of the hardest problems in computing, such as large-scale combinatorial optimizations, by exploiting different operating mechanisms than standard digital computers. We present a scalable optical processor with electronic feedback that can be realized at large scale with room-temperature technology. Our prototype machine is able to find exact solutions of, or to sample good approximate solutions to, a variety of hard instances of Ising problems with up to 100 spins and 10,000 spin-spin connections.