A new quantum-cryptography scheme to secure anonymous transactions
March 13, 2014

In the future, quantum cryptography might secure transactions such as identification at ATMs, as in this artist’s impression (credit: CQT, National University of Singapore)
An international team has demonstrated a form of quantum cryptography that can protect people doing business with others they may not know or trust – a situation encountered often on the Internet and in everyday life — for example, at a bank’s ATM.
“I expect that quantum technologies will gradually become integrated with existing devices such as smartphones, allowing us to do things like identify ourselves securely or generate encryption keys,” says Stephanie Wehner, a Principal Investigator at Center for Quantum Technologies at the National University of Singapore (CQT) and co-author on the paper in Nature Communications (open-access arXiv version also available.)
CQT theorists Wehner and Nelly Ng teamed up with researchers at the Institute for Quantum Computing (IQC) at the University of Waterloo, Canada, for the demonstration.
Two-party secure computation
Today, taking money out of an ATM requires that you put in a card and type in your PIN. You trust the bank’s machine with your personal data. But what if you don’t trust the machine? You might instead type your PIN into your trusted phone, then let your phone do secure quantum identification with the ATM (see artist’s impression above).
Ultimately, the aim is to implement a scheme that can check if your account number and PIN matches the bank’s records without either you or the bank having to disclose the login details to each other.
In cryptography, the problem of providing such a secure way for two mutually distrustful parties to interact is known as “two-party secure computation.”
Random oblivious transfer (ROT) experiments
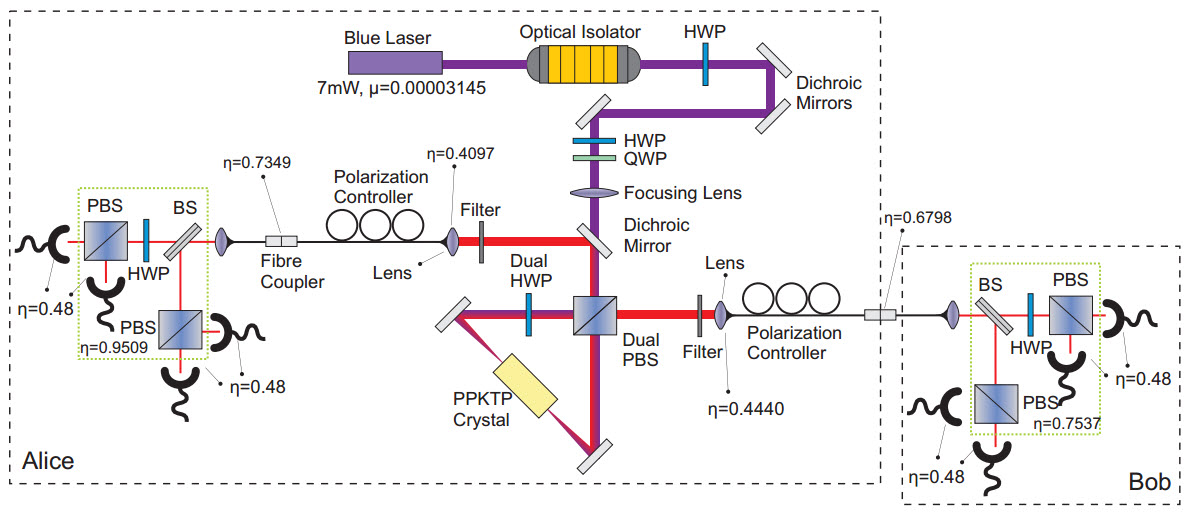
Schematic diagram of random oblivious transfer (ROT) experiment setup (credit: C. Erven et al./arXiv)
The experiments performed at IQC deployed quantum-entangled photons in such a way that one party, dubbed Alice, could share information with a second party, dubbed Bob, while meeting stringent restrictions. Specifically, Alice has two sets of information.
Bob requests access to one or the other, and Alice must be able to send it to him without knowing which set he’s asked for. Bob must also learn nothing about the unrequested set. This is a protocol known as 1-2 random oblivious transfer (ROT).
To start the ROT protocol, Alice creates pairs of entangled photons. She measures one of each pair and sends the other to Bob to measure. Bob chooses which photons he wants to learn about, dividing his data accordingly without revealing his picks to Alice. Both then wait for a length of time chosen such that any attempt to store quantum information about the photons is likely to fail. To complete the oblivious transfer, Alice then tells Bob which measurements she made, and they both process their data in set ways that ensure the result is correct and secure within a pre-agreed margin of error.
In the demonstration performed at IQC, Alice and Bob achieved a random oblivious transfer of 1,366 bits. The whole process took about three minutes.
Secure identification
Unlike current protocols for ROT that use only classical physics, the security of the quantum protocol cannot be broken by computational power.
Its security depends only on Alice and Bob not being able to store much quantum information for long. This is a reasonable physical assumption, given that today’s best quantum memories are able to store information for minutes at most.
Moreover, any improvements in memory can be matched by changes in the protocol: a bigger storage device simply means more signals have to be sent to achieve security.
ROT is a starting point for more complicated schemes that have applications, for example, in secure identification. “Oblivious transfer is a basic building block to make something more fantastic,” says Wehner.
Handheld quantum key distribution devices

The experiment’s Alice and Bob communicated with entangled photons produced in this setup. Such apparatus could be miniaturizzed using techniques from integrated optics. (Credit: IQC, University of Waterloo)
The experiment at IQC adapted devices built to do a more standard form of quantum cryptography known as quantum key distribution (QKD), a scheme that generates random numbers for scrambling communication.
Devices for QKD are already commercially available, and miniaturized versions of this experiment are, in principle, possible using integrated optics.
In the future, people might carry hand-held quantum devices that can perform this kind of feat, the researchers suggest.
“We did the experiment with big and bulky optics taking meters of space, but you can well imagine this technology being shrunk down to sit happily next to classical processing circuits on a microchip.
The field of integrated quantum optics has been progressing in leaps and bounds, and most of the key pieces required to implement ROT have already been successfully demonstrated in integrated setups a few millimeters in size,” says Chris Erven, who performed the experiments at IQC as a PhD student.
An important contribution by Wehner and Ng to the current work was a new way to measure how much Bob might extract from Alice about her second set of information during the protocol. The new min-entropy uncertainty relation, published earlier in Physical Review A, massively reduced the number of entangled photons that had to be measured for the process to succeed. In turn, this reduced the likely duration of the protocol from an impractical number of hours to just a few minutes.
Abstract of Nature Communications paper
Cryptography’s importance in our everyday lives continues to grow in our increasingly digital world. Oblivious transfer has long been a fundamental and important cryptographic primitive, as it is known that general two-party cryptographic tasks can be built from this basic building block. Here we show the experimental implementation of a 1-2 random oblivious transfer protocol by performing measurements on polarization-entangled photon pairs in a modified entangled quantum key distribution system, followed by all of the necessary classical postprocessing including one-way error correction. We successfully exchange a 1,366 bit random oblivious transfer string in ~3 min and include a full security analysis under the noisy storage model, accounting for all experimental error rates and finite size effects. This demonstrates the feasibility of using today’s quantum technologies to implement secure two-party protocols.