Apple’s first AI paper focuses on creating ‘superrealistic’ image recognition
December 28, 2016
Apple’s first paper on artificial intelligence, published Dec. 22 on arXiv (open access), describes a method for improving the ability of a deep neural network to recognize images.
To train neural networks to recognize images, AI researchers have typically labeled (identified or described) each image in a dataset. For example, last year, Georgia Institute of Technology researchers developed a deep-learning method to recognize images taken at regular intervals on a person’s wearable smartphone camera.

Example images from dataset of 40,000 egocentric images with their respective labels (credit: Daniel Castro et al./Georgia Institute of Technology)
The idea was to demonstrate that deep-learning can “understand” human behavior and the habits of a specific person, and based on that, the AI system could offer suggestions to the user.
The problem with that method is the huge amount of time required to manually label the images (40,000 in this case). So AI researchers have turned to using synthetic images (such as from a video) that are pre-labeled (in captions, for example).
Creating superrealistic image recognition
But that, in turn, also has limitations. “Synthetic data is often not realistic enough, leading the network to learn details only present in synthetic images and fail to generalize well on real images,” the authors explain.
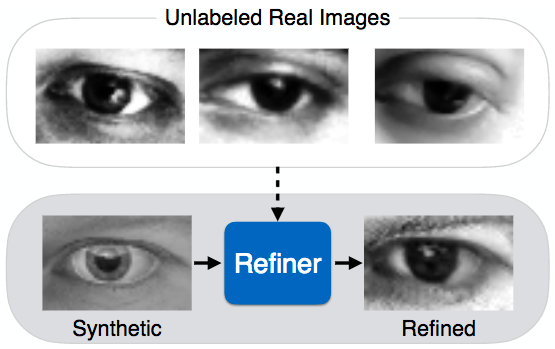
Simulated+Unsupervised (S+U) learning (credit: Ashish Shrivastava et al./arXiv)
So instead, the researchers have developed a new approach called “Simulated+Unsupervised (S+U) learning.”
The idea is to still use pre-labeled synthetic images (like the “Synthetic” image in the above illustration), but refine their realism by matching synthetic images to unlabeled real images (in this case, eyes) — thus creating a “superrealistic” image (the “Refined” image above), allowing for more accurate, faster image recognition, while preserving the labeling.
To do that, the researchers used a relatively new method (created in 2014) called Generative Adversarial Networks (GANs), which uses two neural networks that sort of compete with each other to create a series of superrealistic images.*
A visual Turing test
“To quantitatively evaluate the visual quality of the refined images, we designed a simple user study where subjects were asked to classify images as real or refined synthetic. Each subject was shown a random selection of 50 real images and 50 refined images in a random order, and was asked to label the images as either real or refined. The subjects found it very hard to tell the difference between the real images and the refined images.” — Ashish Shrivastava et al./arXiv
So will Siri develop the ability to identify that person whose name you forgot and whisper it to you in your AirPods, or automatically bring up that person’s Facebook page and latest tweet? Or is that getting too creepy?
* Simulated+Unsupervised (S+U) learning is “an interesting variant of adversarial gradient-based methods,” Jürgen Schmidhuber, Scientific Director of IDSIA (Swiss AI Lab), told KurzweilAI.
“An image synthesizer’s output is piped into a refiner net whose output is classified by an adversarial net trained to distinguish real from fake images. The refiner net tries to convince the classifier that it’s output is real, while being punished for deviating too much from the synthesizer output. Very nice and rather convincing applications!”
Schmidhuber also briefly explained his 1991 paper [1] that introduced gradient-based adversarial networks for unsupervised learning “when computers were about 100,000 times slower than today. The method was called Predictability Minimization (PM).
“An encoder network receives real vector-valued data samples (such as images) and produces codes thereof across so-called code units. A predictor network is trained to predict each code component from the remaining components. The encoder, however, is trained to maximize the same objective function minimized by the predictor.
“That is, predictor and encoder fight each other, to motivate the encoder to achieve a ‘holy grail’ of unsupervised learning, namely, a factorial code of the data, where the code components are statistically independent, which makes subsequent classification easy. One can attach an optional autoencoder to the code to reconstruct data from its code. After perfect training, one can randomly activate the code units in proportion to their mean values, to read out patterns distributed like the original training patterns, assuming the code has become factorial indeed.
“PM and Generative Adversarial Networks (GANs) may be viewed as symmetric approaches. PM is directly trying to map data to its factorial code, from which patterns can be sampled that are distributed like the original data. While GANs start with a random (usually factorial) distribution of codes, and directly learn to decode the codes into ‘good’ patterns. Both PM and GANs employ gradient-based adversarial nets that play a minimax game to achieve their goals.”
[1] J. Schmidhuber. Learning factorial codes by predictability minimization. Technical Report CU-CS-565-91, Dept. of Comp. Sci., University of Colorado at Boulder, December 1991. Later also published in Neural Computation, 4(6):863-879, 1992. More: http://people.idsia.ch/~juergen/ica.html