World’s largest quantum computation uses 84 qubits
January 12, 2012
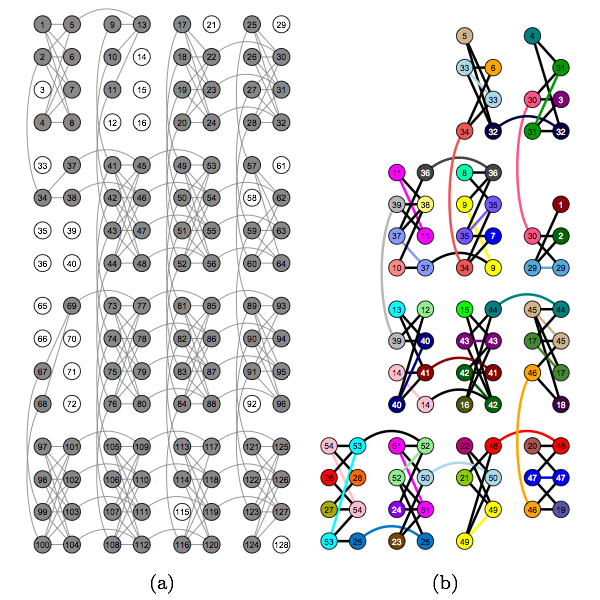
(a) Layout of qubits and couplers, (b) embedding for qubit connectivity (credit: Zhengbing Bian et al.)
D-Wave Systems has carried out a calculation involving 84 qubits on its D-Wave One quantum computing system, Technology Review Physics arXiv blog reports.
Their complex task was to calculate various “two-color Ramsey numbers,” connected with the emergence of order in disordered systems.
Ref.: Zhengbing Bian et al., Experimental Determination Of Ramsey Numbers With Quantum Annealing, arxiv.org/abs/1201.1842