Multi-party quantum communication now possible, physicists demonstrate
March 26, 2014

Photons generated in the lab were beamed to separate trailers in field on the University of Waterloo campus. The experiment proved quantum nonlocality. (Credit: University of Waterloo)
Physicists at the Institute for Quantum Computing (IQC) at the University of Waterloo have demonstrated the distribution of three entangled photons at three different locations (Alice, Bob, and Charlie) several hundreds of meters apart for the first time, proving quantum nonlocality for more than two entangled photons.
The findings of the experiment, Experimental Three-Particle Quantum Nonlocality under Strict Locality Conditions, are published in Nature Photonics.
Overcoming the ‘locality loophole’
Once described by Einstein as “spooky action at a distance,” this three-photon entanglement leads to interesting possibilities for multi-party quantum communication.
Nonlocality describes the ability of particles to instantaneously know about each other’s state, even when separated by large distances. In the quantum world, this means it might be possible to transfer information instantaneously — faster than the speed of light. This contravenes what Einstein called the “principle of local action,” the rule that distant objects cannot have direct influence on one another, and that an object is directly influenced only by its immediate surroundings.
But what if hidden local variables are actually responsible for the correlation between the three photons; that is Einstein was right? To determine that, IQC scientists needed the experiment to close what is known as the “locality loophole.” To do that, they had to separate the entangled photons in a way that did not allow for a signal to coordinate the behavior of the photons.
So they beamed the entangled photons to trailers parked in fields several hundred meters from their lab. To ensure the locality loophole was closed, random-number generators measured the timing of the photon at each trailer independently. The time tagging devices also ensured that the measurements happened in a very small time window (three nanoseconds).
Since light only travels .9 meters in that period of time, no information could possibly be transmitted from one location to the other over a distance of hundreds of meters during the measurement period — a critical condition to prove the non-locality of entanglement.*
A network of people connected by quantum communication devices
The experiment demonstrated the distribution of three entangled particles, which can eventually be used to do more than pairwise communication where only one party can communicate with another. It opens the possibility for multipartite quantum communication protocols, including Quantum Key Distribution (QKD), third man cryptography, and quantum secret sharing.
“The interesting result is that we now have the ability to do more than paired quantum communication,” said the paper’s lead author Chris Erven, a former IQC PhD student who is now a research assistant at the University of Bristol.
“QKD, so far, has been a pairwise system — meaning that it works best and with less assumptions when you’re only talking with one other person. This is the first experiment where you can now imagine a network of people connected in different ways using the correlations between three or more photons.”
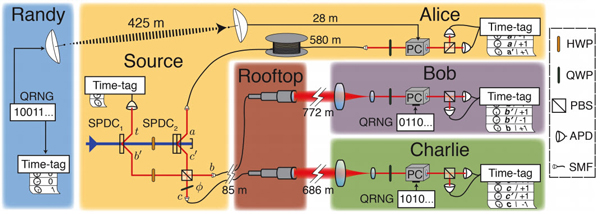
* The project team studied the correlations of three photons in a Greenberger-Horne-Zeilinger (GHZ) state — a type of entangled quantum state involving at least three particles. First, photon triplets were generated in Resch’s lab — the Alice in the experiment.
Then, the first photon was delayed in a 580m optical fibre in the lab while the two other photons travelled up 85m of optical fibre to the rooftop where they were sent through two telescopes. Both photons were then sent to two trailers, Bob and Charlie, about 700m away from the source and from each other.
To maintain the spacelike separate in the experiment, a fourth party, Randy, located in a third trailer randomly selected each of the measurements that Alice was to perform on her photons in the lab.
Each trailer contained detectors, time-tagging devices developed by IQC spin off company Universal Quantum Devices (UQD), and quantum random number generators.
Abstract of Nature Photonics paper
Quantum correlations, often observed as violations of Bell inequalities, are critical to our understanding of the quantum world, with far-reaching technological and fundamental impact. Many tests of Bell inequalities have studied pairs of correlated particles. However, interest in multi-particle quantum correlations is driving the experimental frontier to test larger systems. All violations to date require supplementary assumptions that open results to loopholes, the closing of which is one of the most important challenges in quantum science. Seminal experiments have closed some loopholes, but no experiment has closed locality loopholes with three or more particles. Here, we close both the locality and freedom-of-choice loopholes by distributing three-photon Greenberger–Horne–Zeilinger entangled states to independent observers. We measured a violation of Mermin’s inequality with parameter 2.77 ± 0.08, violating its classical bound by nine standard deviations. These results are a milestone in multi-party quantum communication and a significant advancement of the foundations of quantum mechanics.
————————————————————————————–
Quantum Optics and Quantum Information group site led by Kevin Resch
Quantum Photonics Laboratory that developed the many pieces of the experiment led by Thomas Jennewein