What is the optimal size of a power grid?
April 14, 2014
David Newman, a physicist at the University of Alaska, believes that smaller grids would reduce the likelihood of severe outages, such as the 2003 Northeast blackout that cut power to 50 million people in the United States and Canada for up to two days.
Newman and co-authors make their case in the journal Chaos.
North America has three power grids that transmit electricity from hundreds of power plants to millions of consumers. Each grid is huge, because the more power plants and power lines in a grid, the better it can even out local variations in the supply and demand or respond if some part of the grid goes down.
But large grids are vulnerable to the rare but significant possibility of a grid-wide blackout like the one in 2003, when overloaded transmission lines hit unpruned foliage in Ohio, combined with a software bug a power-plant alarm system.
“The problem is that grids run close to the edge of their capacity because of economic pressures. Electric companies want to maximize profits, so they don’t invest in more equipment than they need,” Newman said.
On a hot days, when everyone’s air conditioners are on, the grid runs near capacity. If a tree branch knocks down a power line, the grid is usually resilient enough to distribute extra power and make up the difference. But if the grid is already near its critical point and has no extra capacity, there is a small but significant chance that it can collapse like a sandpile.
This is vulnerable to cascading events comes from the fact that the grid’s complexity evolved over time. It reflects the tension between economic pressures and government regulations to ensure reliability.
Backup Power Versus Blackout Risk
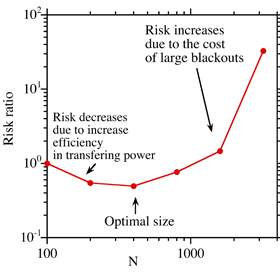
The overall operational “Risk” as a function of the system size (N), showing a decrease at first as the system becomes more efficient with size followed by an increase as the risk of large failures starts to dominate. The optimal size is then the minimum point in the curve. (Credit: B.A. Carreras/BACV Solutions)
In their new paper, the researchers ask whether the grid has an optimal size, one large enough to share power efficiently but small enough to prevent enormous blackouts.
The team based its analysis on the Western United States grid, which has more than 16,000 nodes. Nodes include generators, substations, and transformers (which convert high-voltage electricity into low-voltage power for homes and business).
The model started by comparing one 1,000-bus grid with ten 100-bus networks. It then assessed how well the grids shared electricity in response to virtual outages.
“We found that for the best tradeoff between providing backup power and blackout risk, the optimal size was 500 to 700 nodes,” Newman said.
Though grid wide blackouts are highly unlikely, they can dominate costs. They are very expensive and take longer to get things back under control. They also require more crews and resources, so utilities can help one another as they do in smaller blackouts.
In smaller grids, the blackouts are smaller and easier to fix because utilities can call for help from surrounding regions. Overall, small grid blackouts have a lower cost to society,” Newman said.
The researchers believe their insights into sizing might apply to other complex, evolved networks like the Internet and financial markets.
“If we reduce the number of connected pieces, maybe we can reduce the societal cost of failures,” Newman added.
Abstract of Chaos: An Interdisciplinary Journal of Nonlinear Science paper
Failures of the complex infrastructures society depends on having enormous human and economic cost that poses the question: Are there ways to optimize these systems to reduce the risks of failure? A dynamic model of one such system, the power transmission grid, is used to investigate the risk from failure as a function of the system size. It is found that there appears to be optimal sizes for such networks where the risk of failure is balanced by the benefit given by the size.